[GNN] 4-1. Recurrent Graph Neural Networks (RecGNNs)

[GNN] 4-1. Recurrent Graph Neural Networks (RecGNNs)

 

 

1. Graph란?

- 왜 Graph?

- Graph의 종류

- Graph의 표현

- Graph Tasks

- Graph의 Motif 

 

 

2. Graph Representation Learning 

- Node Embedding

- Graph Embedding 

 

 

3. GNN 이전의 Graph 학습 

- Node Feature

• Eigenvector centrality
• Betweenness centrality
• Closeness centrality
• .....

- Link Feature

• Distance-based feature
• Local neighborhood overlap
• Global neighborhood overlap

- Graph Feature

• Graphlet kernel
• Weisfeiler-Lehman Kernel 

 

4. GNN

- Recurrent Graph Neural Networks (RecGNNs)

- Convolutional Graph Neural Networks (ConvGNNs)

• Spectral Model
• Spatial Model 

- Graph AutoEncoders (GAEs) 

• Network Embedding
• Graph Generation

- Spatial-Temporal Graph Neural Networks (STGNNs)

• CNN Based 
• RNN Based
• CNN & RNN based Model 
• Attention based Model 

 

5. GNN의 Benchmark Datasets

- Citation Networks

- Biochemical Graphs

- Social Networks 

- Others

 

 

6. GNN Library

- Pytorch Geometric

- DGL 

 

 

 

---

 

 

Graph Neural Networks 가 recurrent 모델로부터 출발하였다. 그래프 자체가 시작과 끝이 있는 것이 아닌, 순환 구조이기 때문에 이 구조를 recurrent 모델을 통해 표현하고자 한 것으로 생각된다.

 

 

 

RecGNN은 노드 표현을 RNN으로 학습하고자 하는 것에 중점을 둔다. 여기서는 노드가 stable equilibrium에 도달할 때 까지 계속해서 정보/메시지를 이웃 노드와 교환한다고 전제하였다. 이를 Message Passing이라고도 한다. 

 

RecGNN은 다음에 등장하는 ConvGNN에 많은 영향을 주었다는 점에서 의미가 있다. 특히 이 message passing이라는 아이디어는 spatial-based convolutional GNN 에서도 이어졌다.

 

또한 과거에는 컴퓨터의 연산 능력의 한계로 주로 방향성 그래프에 대해서만 연구되었다. RecGNN은 고수준의 node representation을 추출하기 위해 노드들의 파라매터들을 재귀적으로 적용한다.

 

 

RecGNNs

 

 

1. Learning representations by back-propagating errors (1997)

2.1 A new model for learning in graph domains (2005) 2.2 The graph neural network model, GNN (2008)

3. Graph Echo State Networks, GraphESN (2010)

4. Gated graph sequence neural networks, GGNN (2015)

5. Stochastic Steady-state Embedding, SSE (2018

 

 

 

RecGNN의 발전 과정

 

 

 

 

1. Learning representations by back-propagating errors (1997)

 

neural network static infromation or temporal sequence structure data 에는 잘 되지만 graph 같은 structure data에는 잘 안된다. 그 이유는 graph의 경우 structure 사이즈가 다양하기 때문이다. 그래서 이러한 사이즈의 변화에도 사용할 수 있는 방법인 generalized recursive network를 제안했다. 하지만 computational limitation이 존재한다. 또한, directed graph에만 적용 가능하다는 단점이 있다.

 

 

 

2.1 A new model for learning in graph domains (2005) 2.2 The graph neural network model, GNN (2008)

 

 

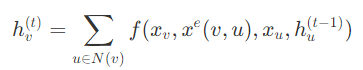
이후 GNN 이라는 단어를 처음 사용한 논문이 공개 되었다. 97년도에 발표된 generalized recursive network와는 달리 directed, undirected, cycle이 있는 그래프 모두 적용 가능하다.

 

또한, 앞선 문제였던 computational complexity를 O(m)으로 줄였다. 여기서 m은 edge 수를 말한다. 즉, edge가 늘어남에 따라 complexity 또한 선형적으로 증가함을 말한다. 이유는 잘 모르겠지만 2005년에 처음 GNN을 소개했는데 앞선 논문에 더해서 time complextity를 줄이는 내용을 더 디테일하게 소개하며 2008년에 두 명의 저자가 추가되어 또 발표했다. 이 GNN 논문에서는 노드의 hidden state를 위와 같이 재귀적으로 업데이트한다.

 

학습 방법은 이웃 노드들의 information을 recurrent하게 전달하여 node state를 업데이트 한다. 이 과정을 node state가 수렴할 때까지 iteration을 반복해야 한다. 여기서 f는 결국 어떤 매개변수를 가진 함수, 즉 쉽게 얘기해서 뉴럴넷을 나타내고, h_v^0은 랜덤하게 초기화된다. 여기서 합계 연산을 통해 모든 노드에 GNN을 적용할 수 있다. 이 공식이 수렴하기 위해서는 재귀 함수인 f가 축약 매핑(contraction mapping)이 되어야 한다는 조건이 있다. 어쨌든 수렴이 된다고 하면, 마지막 step에서 노드의 hidden state 값들이 readout layer로 들어가게 된다.

 

 

 

 

3. Graph Echo State Networks, GraphESN (2010)

 

 

GraphESN을 간단히 설명하자면 encoder와 output layer로 구성되어 있고,

encoder를 통해 전체 graph를 나타내는 값으로 변환한 뒤 고정한다. 이름과 같이 고정된 encoder를 echo로서 언급한 듯 하다.

 

encoder를 학습하는 방법은 contractive state transition function을 통해 recurrent하게 노드를 업데이트하며 global graph state가 수렴할 때까지 반복한다.

 

 

 

 

4. Gated graph sequence neural networks, GGNN (2015)

 

 

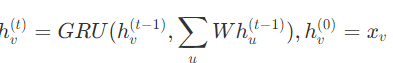
이전에는 수렴할 때까지 iteration을 반복해야 한다는 단점이 있었지만,

GGNN은 step 수를 고정해서 학습하기 때문에 convergence를 위한 iteration parameter가 없다는 것이 장점이다.

또한 이름에서와 같이 recurrent function으로 gated recurrent unit (GRU)을 사용하였다. 이럴 경우에 더이상 수렴을 위해 파라미터들을 제한시키지 않아도 된다는 장점이 있다. hidden state 공식은 위와 같다.

 

이전 GNN과 GraphESN 과의 차이점이라면 back-propagation through time (BPTT)를 사용했다는 것이지만 이러한 방법이 단점이 되기도 한다. Large scale 모델의 경우 모든 node에 대해 intermediate state를 가지고 있어야 하기 때문에, 다시 말해 GGNN이 모든 노드에 대해 재귀 함수를 여러번 실행하려면 모든 노드의 중간 상태들이 전부 메모리에 저장되어야 하기 때문에 memory가 많이 필요하다는 게 흠이다.

 

 

 

 

5. Stochastic Steady-state Embedding, SSE (2018)

 

 

SSE는 앞선 large sacle 모델에 대한 메모리 문제점을 해결할 수 있는 방법이다. Node의 hidden state를 stochastic 방식으로 업데이트 하기 때문에 node를 배치로 샘플링해서 업데이트 할 수 있고 gradient 또한 마찬가지로 배치 단위로 계산한다.

 

하지만 이러한 배치 단위의 학습이 stability를 낮출 수 있는데 이전 state와 현재 state에 가중 평균을 적용해서 stability를 높였다.

 

 

 

Reference

 

 

https://tootouch.github.io/research/gnn_summary/#roadmap

Graph Neural Network 찍어먹기

https://thejb.ai/comprehensive-gnns-1/

Graph Neural Networks 개념정리 1 - 개요

https://thejb.ai/comprehensive-gnns-2/

Graph Neural Networks 개념정리 2 - Recurrent GNN