How Powerful are Graph Neural Networks? (GIN) 정리

 

How Powerful are Graph Neural Networks? (GIN) 정리 

 

 

 

 

 

들어가기 전에....

 

이 부분은 논문의 2. Preliminaries에 해당되는 내용이나, 먼저 알고 가는 것이 논문 이해에 도움이 되어 먼저 작성합니다. 

 

먼저 MPNN에 대해서 설명을 드리고, 이어서 WL test에 대해서 설명드리도록 하겠습니다.

 

 

 

 

1. MPNN

 

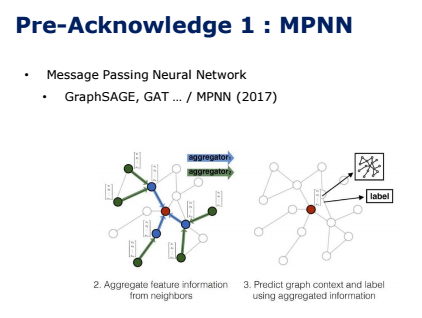
지난 시간과 지지난 시간에 살펴보았던 GraphSAGE나 GAT와 같은 spatial 기반의 방법들은 노드들의 spatial 관계를 활용하여 학습하는 방법으로, convolution 과정을 통해서 주변 노드의 representation(feature vector)만을 학습하여 중심 노드의 representation을 업데이트 하는 방식을 사용합니다. 이런 방식을 Message Passing을 했다, 또는 Neighbor Aggregation했다고 표현합니다. 그리고 이 매커니즘을 사용한 GNN을 MPNN, 풀어서 말하면 Message Passing Neural Network라고도 하게 됩니다. 

 

아래의 그림은 GraphSAGE 논문에서 가져왔는데요, 이러한 Message Passing의 과정을 잘 나타내고 있습니다. 주변 노드들에서 feature 정보들을 aggregate하여, 중심 노드의 feature를 업데이트하는 방식이 됩니다.

 

 

 

 

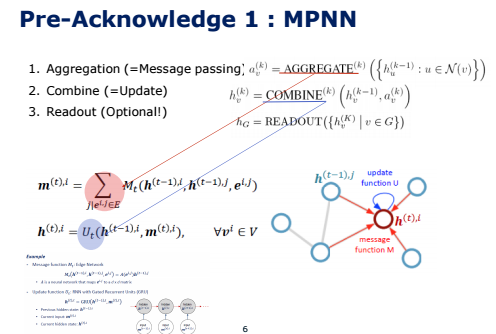
이 MPNN 모델들의 과정을 3단계로 일반화할 수 있겠습니다. 주변 노드들의 feature를 모으는 Aggregation 단계, 이를 이용해서 중심 노드에 반영하는 Update 단계가 있습니다. 각 모델마다 Aggregate할 때 어떤 함수를 사용하는지, 또는 Update할 때 어떤 함수를 사용할지 각각 조금씩 차이가 있습니다.

 

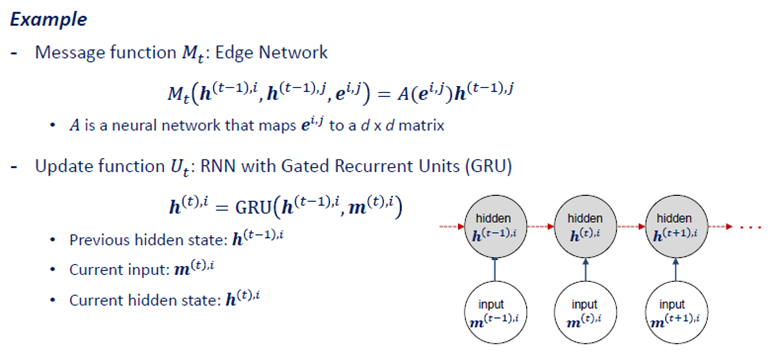
아래의 그림은 한 예시인데요, 이 예시 모델에서는 Aggregate함수로써 Sum을 사용했고, Update함수로는 GRU를 사용했다고 합니다. 이렇게 모델마다 어떤 함수를 쓰느냐에 따라 Architecture가 차이가 있다고 볼 수 있습니다.

 

GNN의 표현력을 키우는 문제는 결국 aggregation을 어떻게 구성하냐와 관련되어 있기 때문에, 뒤에서 GIN이 어떻게 Aggregate하는지를 집중해서 보시면 좋을 것 같습니다.

 

 

 

 

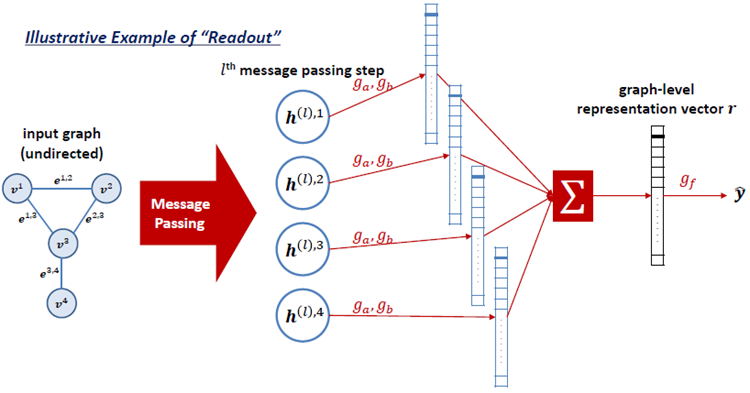
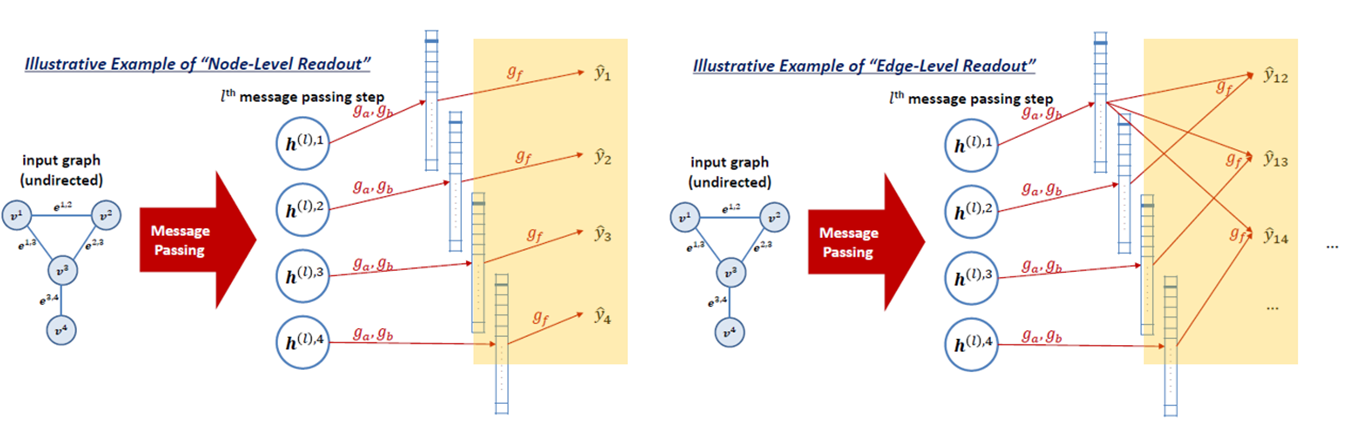
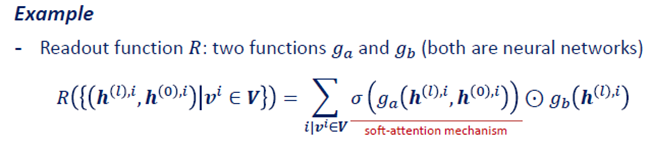
마지막으로 Readout Function에는 왜 Optional라고 써놓았냐면, 이 Readout Function은 output이 Graph level에서 나오는 task에서만 사용되기 때문입니다. 여기서 “readout function”이란 노드의 hidden representation을 통해 전체 graph의 representation을 뽑는 역할을 합니다. 

 

1번과 2번 과정을 거쳐서, 각 노드에 대해 hidden representation을 계산한 후에는 이 값에 output layer를 붙여서 node-level prediction 문제를 풀 수도 있지만, readout function을 사용해서 전체 graph-level prediction 문제를 풀 수도 있습니다. 

 

일반적으로 readout은 모두 graph classification task에서만 사용하고, 이 또한 앞의 aggregate함수나 update함수처럼, 어떤 함수를 사용하는지는 모델마다 조금씩 차이가 있게 됩니다. Graph representation hG 가 node 의 ordering 에 따라 달라지지 않아야하기 때문에, Permutation invariant function만 사용할 수 있습니다. 이 특징은 Readout함수를 설정하는데 있어 큰 특징이 되게 됩니다.  Permutation invariant function 에는 Sum, mean, min, max도 있지만, neural network을 활용하여 learnable한 경우도(graphSAGE의 lstm aggregator) 있다고 합니다. 그래서 GIN은 어떻게 Aggregate 함수와 readout 함수를 설정했나?를 중점적으로 보시면 됩니다!!!

 

(MPNN은 soft attention mechanism를 사용했대, 근데 이게 어떻게 permutation invariant해지는지 궁금하다! https://arxiv.org/pdf/1704.01212.pdf 이 논문에 3번 )

 

 

 

 

 

 

2. Weisfeiler-Lehman Test

 

 

GIN 논문에서 핵심적인 역할을 하는 WL test에 대해 설명하기에 앞서서, GNN 이전에는 어떻게 Graph에 대해 정보를 추출하고 학습했는지 말씀드려야 할 것 같습니다.

 

Machine Learning Tasks를 수행하기 위해서는 Node, Link, Graph를 feature로 만드는 것이 중요합니다. 그래서 각각의 그 특성에 따라 feature를 뽑아내는 방법들이 아래와 같이 다양하게 있습니다. 특히 Graph의 feature를 뽑아낼 때는 두 개의 그래프간의 유사성을 측정하는 Graph Kernel 방식을 사용하고, 우리가 살펴보고자 하는 이 WL test는 Graph Level에서 feature를 뽑아내는 방식입니다.

 

저는 WL test에서만 설명을 드릴 것이지만, 위에 제시된 예전의 method들 또한 graph 분야에서 많이 본 기억이 있어서 혹시 궁금하신 분들은 더 찾아보시면 공부를 하실 때 도움이 될 거라 생각합니다.

 

 

 

 

 

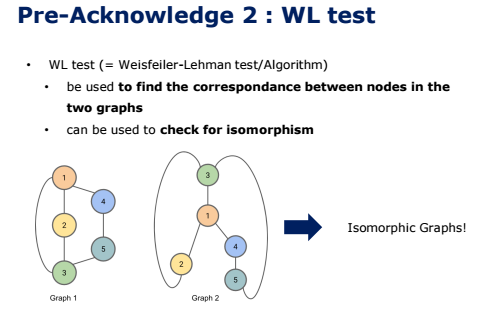
이 Weisfeiler-Lehman test는 두 개의 그래프 간의 유사성을 측정하는 방법 중에서도, 주어진 두 그래프가 isomorphic 한지를 확인하는 방법입니다. 

Isomorphic graph는 한국말로 하면 동형 그래프라는 의미인데, 두 그래프가 똑같은 node와 똑같은 edge로 구성되어 있다면, 두 그래프를 동형 그래프라고 합니다.아래의 그림에서도 겉보기엔 달라보이지만, 두 그래프가 똑같은 node와 똑같은 edge로 구성되어 있기 때문에 동형 그래프라고 할 수 있습니다.

이 WL Test는 몇몇 극단적인 예시를 제외하고는 Graph의 broad class를 구별하는 가장 효과적인 테스트로 평가받고 있습니다. 따라서 본 논문에서는 이 WL test의 성능을 따라갈 수 있는 GNN model을 만들고자 했습니다.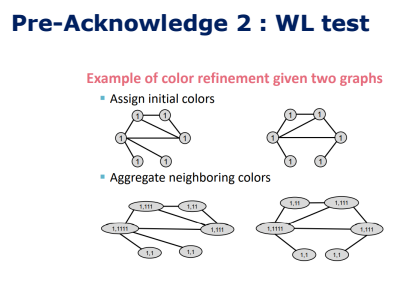 

 

WL test는 Color refinement라고 불리는 Algorithm을 활용하여 나타냅니다.

우선 위 그림처럼 colors를 초기화 한 후 인접 노드의 colors를 추가합니다.

 

후에 위 그림처럼 Aggregated colors를 Hash table에 새로운 컬러로 맵핑합니다.

 

 

다시 앞에서와 같은 동일한 과정을 반복합니다. 이렇게 반복하는 것은 저희가 GNN에서 주변 노드의 정보들을 받아와 중심 노드로 update를 반복하는 과정과 일맥상통하다고 보시면 됩니다.

 

 

 

왼쪽 그림처럼 각 colors의 개수를 셉니다.

 

오른쪽 그림처럼 두 color count vectors를 내적하면 WL kernel value를 계산할 수 있습니다.

 

이 알고리즘은 만약 일정 수준의 반복 이후 2개의 Graph에 존재하는 Node들의 Label이 달라지게 되면 2개의 Graph는 non-isomorphic 하다고 판단하게 됩니다.

이런 방법으로 두 graph가 동형인지 아닌지 판단합니다.

Weisfeiler-Lehman Kernel은 시간 복잡도가 선형이기 때문에 다른 kernel보다 매우 효율적인 방법입니다.

이 WL test는 현존하는 GNN 모델보다 더 그래프에 대해 잘 표현한다고 하는데요, 그 이유를 뒤에서 설명 드리도록 하겠습니다.

 

 

 

 

 

 

1. Introduction

 

 

 

이 GIN 논문을 딱 한 줄 요약하자면, 어떻게 GNN 모델이 그렇게 풍부한 그래프 표현력을 가지게 되었고, 어떻게 하면 그 그래프 표현력을 극대화한 모델, 즉, GNN 모델이 가질 수 있는 가장 효율적인 구조를 디자인 할 수 있을까?를 연구한 논문입니다.

그럼 어떤 게 좋은 그래프 표현력일까? 라는 의문이 들게 되는데요, 그렇다면 gnn의 노드 임베딩은 local neighborhood structure를 어떻게 구분하고, 얼마나 구분할 수 있을까? 구분하지 못하는 상황은 언제 발생할까? 에 대한 것을 그림을 통해 살펴보도록 하겠습니다.

 

 

 

 

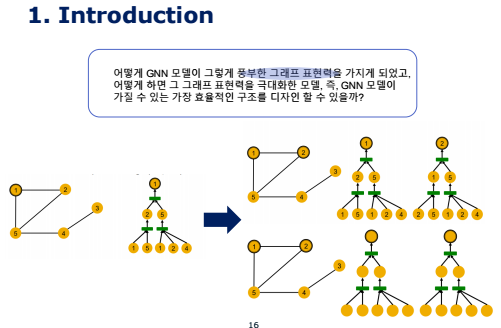
gnn의 각 레이어마다 이웃노드의 정보를 취합하고 이를 가공해서 새로운 노드 임베딩을 생성한다는 점을 떠올렸을 때, 이는 결국 gnn은 이웃 노드를 바탕으로 정의된 계산 그래프를 따라서 정보가 흘러가고, 이를 통해 임베딩 레이어가 생성된다는 것을 의미합니다.

 

위의 그래프에서 1번 노드를 기준으로 2-hop 이웃노드까지 고려한다고 하면, 결국 2-hop에서부터 시작하여 계산 그래프를 구성하면 1번 노드에 대한 노드 임베딩을 생성하는 과정이 그려지게 됩니다.

이걸 모든 노드에 대해서 진행해보면  문제가 발생하는데, 동일한 계산 그래프 구조를 가지는 경우가 생깁니다.

 

다시 말하자면, 오른쪽 위의 그림에선 임의로 노드에 id를 부여하고 있어서 1번 노드에 대한 트리와 2번 노드에 대한 트리가 달라보이지만, 각 노드에 대한 저 숫자 정보는 모델에게는 주어지지 않는 정보입니다. 그래서 사실상 모델이 각 노드에 대해서 임베딩을 했을 때는 모델은 트리 구조를 오른쪽 위의 그림이 아닌 아래의 그림과 같이 받아들이게 됩니다. 이렇게 되면 1번 노드에 대한 트리와 2번 노드에 대한 트리를 구별할 수 없게 됩니다. 즉, 모델의 입장에서 각 노드가 노드 자체만으로는 구별할 수 없다는 것을 의미합니다. 

 

 

 

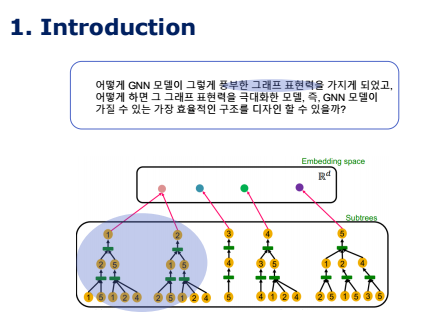
gnn은 결국 각 노드를 root로 한 작은 트리 구조에서 노드 임베딩을 구성하자면 위와 같습니다. 

아까 앞에서 보았던 1번 노드의 트리 구조와 2번 노드의 트리 구조를 gnn에서는 구분하지 못하기 때문에, 즉 같은 트리라고 취급하기 때문에, 같은 임베딩 값을 갖게 됩니다.

즉, 위의 질문에 대한 대답은, 표현력이 좋은 gnn이라면 다른 트리 구조를 가지는 노드에 대해 항상 다르게 임베딩할 것을 의미합니다. 다시 말해  가장 표현력이 좋은 gnn이라 함은 계산 그래프를 입력으로 하고, 다른 계산그래프에 대해 각각 다른 임베딩 벡터를 출력하는 함수가 가장 표현력이 좋은 GNN이라고 할 수 있습니다. 이렇게 다른 계산그래프에 대해 각각 다른 임베딩 벡터를 출력하는 함수를 논문에서는 injective function, 일대일 함수라고 말합니다. Injective function이 이 논문에서는 아주 중요한 개념이라 기억에 남겨두셨으면 좋겠습니다.

 

 

 

 

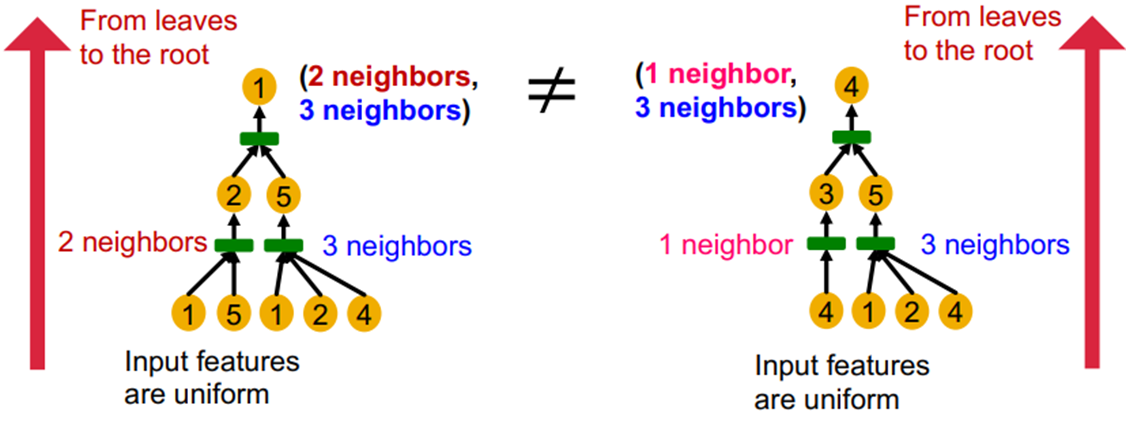
좀더 gnn을 자세히 보자면, 동일한 높이를 가지는 계산그래프는 가장 아래단의 잎 노드에서 뿌리 노드까지 반복(recursively)적으로 정보가 처리되면서 구분되게 됩니다. 예를 들어 위의 그림에서 왼쪽 트리와 오른쪽 트리는 각각의 자식 노드가 다른 이웃노드의 수를 가지기 때문에, 다른 노드라고 구분하는 것과 같습니다.

 

이를 좀 더 자세히 보면, 반복적으로 정보가 처리되는 구간은 aggregation function입니다. 즉, gnn의 aggregation function이 일대일 함수 라면, 최대한 이웃노드의 정보를 살리면서 노드를 임베딩하게 되므로, 가장 표현력이 좋은 gnn이 될 수 있습니다. 그래서 앞서서 살펴본 Aggregate, update, readout 이렇게 세 단계 중 Aggregate함수를 어떻게 지정하느냐, 특히 Aggregate 함수가 일대일 함수가 GNN 자체의 성능을 결정하는 큰 요인이 됩니다.

 

앞에서 WL test가 현존하는 GNN보다 표현력이 가장 좋다고 말씀드렸는데요, 그 이유는 앞에서 보셨던 WL test의 aggregation 함수가 hash table이기 때문에 일대일 함수이기 떄문입니다. 일대일 함수라는 것은 다시 말씀드리자면, 만약에 그래프의 두 node가 서로 다른 neighborhood 를 가지고 있다면, 서로 다른 label 을 가지게 된다는 것입니다.  따라서 오늘 설명드릴 GIN은 aggregation 함수가 표현력에 중요한 역할임을 증명하고 WL test의 성능에 조금이라도 더 근접하고자 하는 시도를 합니다.

 

앞에서 말씀드린 것처럼 GNN에 Readout function을 덧붙여서 전체 Graph Representation을 뽑아낼 수 있습니다. 이 output으로 나온 Graph Representation이 성능이 얼마나 좋은지를 앞에서 말씀드린 WL test와 성능을 비교함으로써 GNN의 Graph 표현력을 평가 할 수 있을 것이라는 것이 이 논문의 핵심이 됩니다.

 

또한 WL test의 알고리즘이 GNN와 유사하기 때문에 GNN이 WL test의 결과값과 유사하게 나오는 것을 최대한 목표로 하게 됩니다. WL Test도 GNN과 비슷하게,  Node가 주어졌을 때, 이 Node의 이웃들의 Feature 벡터를 통합하여 Node Feature 벡터를 반복적으로 업데이트합니다.

 

WL test 는 일부 극단적인 그래프를 제외하고는, 대부분의 그래프를 구분해낼 수 있습니다 (up to isomorphism). 그 이유는, 바로 알고리즘에서 neighborhood aggregation 이후 node 의 feature vector 를 update 하는 과정이 injective 하기 때문입니다. 여기서 injective라는 건 일대일 함수의 관계를 갖게 된다는 의미로, 만약에 그래프의 두 node가 서로 다른 neighborhood 를 가지고 있다면, 서로 다른 label 을 가지게 됩니다. 반대로 두 노드가 같은 neighborhood를 갖게 되면 같은 label을 가지게 됩니다.

 

이 특징 때문에 아까 앞에서 말했던 가장 표현력이 좋은 모델의 조건을 이 WL test가 갖게 됩니다.

 

( WL Test의 경우 다른 Node 이웃들을 다른 Feature 벡터로 매핑하는 Injective Aggregation Update의 존재로 인해 강력한 효과를 지니게 된다. 본 논문에서는 GNN의 Aggregation Scheme이 굉장히 Expressive하고 Injective Function을 모델링할 수 있다면 GNN 또한 WL Test 처럼 굉장히 강력한 Disciminative Power를 지니게 될 것이라고 이야기 하고 있다. )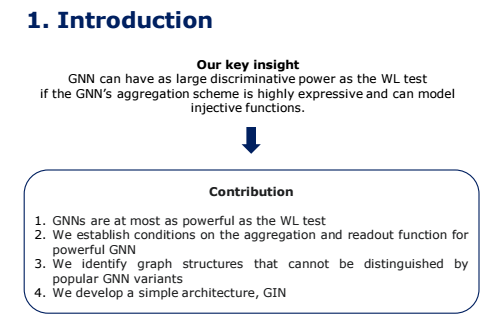

 

우리의 Key insight는 만약 GNN의 aggregate 방식이 충분히 expressive하고 injective function을 modeling할 수 있다면, GNN은 가장 성능이 좋다는 WL test 만큼이나 좋은 discriminative power을 가질 수 있다는 것입니다.

 

그래서 본 논문의 contribution은 GNN은 Graph 구조를 판별하는 데에 있어 WL Test 만큼이나 효과적일 수 있게 하는 Neighbor Aggregation이나 Graph Readout Function의 기준들을 제시합니다.

또한 GCN이나 GraphSAGE는 구분할 수 없는 Graph 구조에 대해 언급하고, GNN 기반의 모델들이 포착할 수 있는 Graph 구조들에 대해 정확하게 분석합니다. 이 모든 것을 바탕으로 GIN이라고 부르는 간단한 신경망 구조를 고안했습니다.

 

3. Theoretical Framework: Overview

 

 

이 section에서는 그 동안의 GNN 모델들에서 사용한 Aggregation Scheme이 injective하지 않고, 그렇기 때문에 덜 powerful하며 Graph의 흥미로운 특징들을 잘 담아내지 못한다는 것을 증명합니다. 그리고 이를 바탕으로 가장 injective한, 표현력이 가장 좋은 GNN model인 GIN을 만들게 됩니다.

 

 

4. Building Powerful Graph Neural Network

 

 

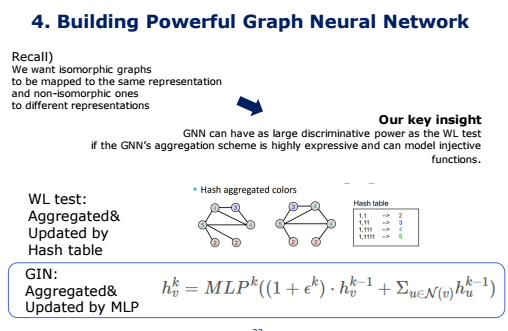
다시 한번 목표를 말하자면, 우리는 동형 그래프는 같은 표현을 가지도록, 비동형이면 다른 표현력을 가진다고 구분하고 싶습니다.

 

앞에서 neighborhood aggregation scheme 을 사용하는 GNN 은 WL test 의 representational power 를 뛰어 넘을 수 없다는 것을 확인할 수 있습니다. 그 대신에 aggregate와 update 함수가 일대일 대응이라면, injective하다면 WL test에 견주는 강력한 표현력을 가질 수 있게 된다고 말씀드렸습니다.

 

GIN은 여기서 WL test에서 사용했던 해쉬 테이블을 MLP로 변형하여 사용합니다. 앞에서 말씀드렸던 것처럼, 해시 테이블은 조금이라도 다른 입력값에 대해서는 전혀 다른 출력을 내는 함수로서 완전히 injective 함수로 동작합니다.

적절한 비선형 함수를 갖는 1-hidden-layer MLP는 일정 수준의 정확도로 어떠한 연속형 함수도 근사할 수 있다는 것이 본 이론의 내용입니다. (이때, 해시 테이블은 조금이라도 다른 입력값에 대해서는 전혀 다른 출력을 내는 함수로서 완전히 단사함수로 동작한다. 또한, k번째 반복에서의 각 노드의 색 변화는 결국 k-hop의 이웃 노드의 정보를 통합한 정보가 될 것이다. )

 

GNN은 반복적으로 이웃 피쳐를 중심 노드에 전달하는 식으로 학습합니다. 하지만, 최초의 반복에서 만약 Input Feature가 One-hot 인코딩이면 그들의 합 또한 injective할 것이기 때문에 합 연산 이전에 MLP가 필요하지는 않습니다. 물론 One-hot 인코딩 되어 있지 않거나 연속형 변수가 중간에 끼어 있다면 MLP가 필요할 것이다. ϵ의 경우 학습 가능한 파라미터 혹은 고정된 스칼라로 둘 수 있습니다. 

최종적으로 GIN은 Node Representation을 아래와 같이 업데이트하게 됩니다. 첫번째 항은 이전 레이어에서의 본인 노드의 벡터일 것이고, 두번째 항은 이웃 노드의 벡터를 종합한 값입니다.

 

 

 

Node classification 에는 GIN 을 바로 사용하면 되지만, graph classification 에는 추가로 graph-level readout function 이 필요합니다. Readout function 은 node 의 feature vector 들에 대한 함수입니다. 이 때 node 의 feature vector (representation) 은 layer 를 거칠수록 local 에서 global 하게 변합니다. Layer 의 수가 너무 많다면, global 한 특성만 남을 것이고, layer 의 수가 너무 적다면 local 한 특성만 가지게 됩니다. 따라서, readout function 을 통해 그래프를 구분하기 위해서는, 적당한 수의 layer 를 거쳐야 합니다.

이런 특성을 반영하기 위해, GIN 은 각 layer 의 graph representation (READOUT(⋅) 의 output) 을 concatenation 으로 모두 합쳐줍니다. 그렇다면 최종 결과는 각 layer 마다 나타나는 그래프의 구조적 정보를 모두 포함하게 됩니다.

따라서, graph classification 에서도 GIN 이 maximally powerful 하다는 것을 알 수 있습니다.

 

 

5. Experiments

 

 

논문에서는 GIN 과 다른 GNN 들의 graph classification 성능을 비교하기 위해, 4개의 bioinformatics datasets (MUTAG, PTC, NCI1, PROTEINS) 와 5개의 social network datasets (COLLAB, IMDB-BINARY, IMDB-MULTI, REDDIT-BINARY, REDDIT-MULTI5K) 에 대해 실험을 수행했습니다.

 

GIN 모델로 (6) 에서 ϵ 을 학습하는 GIN-ϵ 과, ϵ 을 0 으로 고정한 GIN-0 를 선택했습니다. GIN 과 비교하기 위해 (6) 의 summation 을 (9) 와 같이 mean-pooling 또는 max-pooling 으로 바꾸거나, MLP 를 1-layer perceptron 으로 바꾼 모델들 (Figure 4 의 Mean - 1-layer 와 같은 variant 들을 의미합니다.) 을 실험 대상으로 선정했습니다.

Baseline 모델로는 graph classification 의 state-of-the-art 성능을 보여주는 WL subtree kernel, C-SVM, Diffusion-convolutional neural network (DCNN), PATCHY-SAN, Deep Graph CNN (DGCNN), 그리고 Anonymous Walk Embeddings (AWL) 을 사용했습니다.

 

먼저 representational power 를 확인하기 위해 GNN 들의 training accuracy 들을 비교합니다. 모델의 representational power 가 높다면, training set 에서의 accuracy 또한 높아져야 합니다.

 

위 그림에서 모든 데이터 셋에 대하여, GNN보다 WL kernel의 training accuracy가 더 높다는 것을 알 수 있습니다. 앞에서도 말씀드렸듯이, GNN은 WL test보다는 expressive power가 낮기 때문인 것으로 파악됩니다. 이렇게 WL test보다 GNN이 성능이 낮으면 왜 쓰지? 라는 의문을 가지게 되었는데 WL kernel은 graph에서만 적용이 되지, node나 edge feature를 어떻게 결합시킬지는 학습하지 못하기 때문에 GNN을 사용합니다.

 

Figure 4 를 보면 GIN-ϵ 과 GIN-0 모두 training accuracy 가 거의 1 에 수렴하는 것을 볼 수 있습니다. GIN-ϵ 의 경우 각 layer 의 parameter ϵ(k) 또한 학습하지만, GIN-0 와 큰 차이를 보이지는 않습니다. Figure 4 에서 1-layer perceptron 보다는 MLP 를 사용했을 때, mean / max-pooling 보다는 summation 을 사용했을 때 정확도가 대체로 더 높게 나타납니다.

 

Table 1 은 test set 에 대한 classification accuracy 를 보여줍니다. GIN 모델, 특히 GIN-0 모델의 성능이 가장 뛰어나다는 것을 확인할 수 있습니다.

 

 

6. Conclusions

 

 

따라서 최종적으로, 본 논문에서는 GNN은 Graph 구조를 판별하는 데에 있어 WL Test 만큼이나 효과적이라는 것, 즉 GNN의 expressive power을 증명했으며, GNN의 성능을 최대한으로 올릴 수 있는 방법을 연구했습니다.

 

 

 

Until Now...

 

 

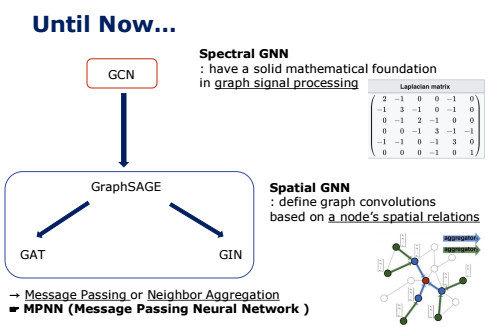
오늘이 GNN 세미나 마지막 시간인데요. 그래서 지금까지 제가 담당한 기본적인 GNN 모델들의 관계나 변화 과정을 요약해 보았습니다.

 

먼저 제일 먼저 등장한 GCN은 Graph에 Convolution를 적용한 모델 중 원조라고 할 수 있습니다.   

이렇게 GCN과 같은 초기의 GNN은 그래프 신호 처리 이론을 기반으로 풀어낸 방식인 Spectral Method를 사용했습니다. Spectral-based 란 스펙트럼에 기반했다는 뜻인데, 여기서 스펙트럼이란 결국 여러가지 파동들의 집합입니다. 하지만 Spectral-based 방식은 기본적으로 무방향 그래프만을 대상으로 하고, 그래프 정보를 normalized graph Laplacian matrix 로 표현하여 사용하기 때문에 그래프의 크기가 커질수록 계산량이 커진다는 한계가 있습니다.

 

이런 한계를 극복하고자 Spatial Method를 사용한 여러 가지 GNN Model들이 등장했습니다. 이미지에서 사용하는 convolution과 유사하게 spatial 기반의 방법들은 노드들의 spatial 관계를 활용하여 학습하는 방법으로, 전체 행렬을 다 다뤄야 하는 Spectral 방식과 달리, convolution 과정을 통해서 중심 노드와 주변 노드의 representation(feature vector)을 학습하여 중심 노드의 representation을 업데이트 하는 방식을 사용합니다. 이런 방식을 Message Passing을 했다, 또는 Neighbor Aggregation했다고 표현합니다. 그리고 이 매커니즘을 사용한 GNN을 MPNN라고도 하게 됩니다. 

 

발전 과정을 살펴보자면, 무방향 그래프만 가능하고 transductive learning만 가능했던 GCN의 한계를 넘기 위해 Spatial 방식을 적용하여 Inductive Learning을 가능하도록 한 GraphSAGE로 발전되었습니다. 하지만 고정된 이웃 노드를 랜덤 샘플링해서 Aggregate하는 방식의 GraphSAGE는 모든 이웃 노드를 고려하지 않기도 하고, 그 이웃들 간의 순서도 반영한다는 한계가 있습니다. 이를 해결하기 위해 GAT에서는 Attention mechanism을 적용해 중심 노드와 연결된 모든 이웃 노드들의 상대적인 가중치까지 학습하는 방식을 사용하게 됩니다. 한편 graphSAGE와 같은 기존의 Spatial 방식에 대한 이론적인 분석을 통해 최적의 구조를 제시하는 방향에서 GIN이 등장하게 됩니다.

 

 

Reference

 

@ GIN 

https://greeksharifa.github.io/machine_learning/2021/06/05/GIN/

Python, Machine & Deep Learning

https://harryjo97.github.io/paper%20review/How-Powerful-are-Graph-Neural-Networks/

How Powerful are Graph Neural Networks?

https://junklee.tistory.com/120

How powerful are Graph Neural Networks [ICLR '19]

https://velog.io/@stapers/Lecture-9-Theory-of-Graph-Neural-Networks

[CS224W] Lecture 9 - Theory of Graph Neural Networks

 

@ MPNN (Message Passing Neural Network)

https://koreapy.tistory.com/392

Graph Neural Networks(GNN) 관련 자료

 

@ WL Kernel (GNN 이전의 Graph Feature 표현하는 방식)

https://velog.io/@tobigsgnn1415/Traditional-Methods-for-Machine-Learning-in-Graphs

2. Traditional Methods for Machine Learning in Graphs

https://harryjo97.github.io/theory/Weisfeiler-Lehman-Algorithm/

Weisfeiler-Lehman Algorithm

https://davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/

The Weisfeiler-Lehman Isomorphism Test | David Bieber

https://asidefine.tistory.com/183

[GNN] 2. GNN 이전의 Machine Learning을 활용한 Graph 학습