Semi-Supervised Classification with Graph Convolutional Networks (GCN) 정리 및 코드 분석

0. 들어가기 전에 

 

1) Graph Representation 

 

 

 

 

 

먼저 GCN을 설명하기 앞서 필요한 개념들을 설명하겠습니다.

그래프는 일반적으로 행렬로 표현합니다.

 

 첫번째로 인접 행렬은 노드 간의 연결 여부를 표현합니다. 차수 행렬은 각 대각 행렬에 어떤 노드의 차수 정보, 즉 연결 edge의 개수만을 표현합니다. 라플라시안 행렬은 차수 행렬에서 인접 행렬을 빼게 되면서 차수 행렬의 정보와 인접행렬의 정보를 모두 담게 됩니다. 식으로 나타내면 위와 같습니다.

 

하지만 이런 표현 방식은, 전체 노드의 개수가 많아질수록 행렬이 너무 커지기 때문에 이후에 그래프 임베딩이라는 개념을 통해 더 작은 차원으로 줄여서 사용합니다.

 

 

라플라시안 행렬을 좀 더 자세히 보겠습니다. 라플라시안 행렬은 단순히 차이만을 구할 수도 있지만 차이에 제곱을 해서 사용할 수도 있습니다. 절댓값 또는 제곱을 취하지 않은 채 difference값들의 단순 합을 통해 부호가 상쇄되므로, h값이 0에 가깝다고 f_i와 neighbor node feature간에 유사도가 크다고 하기 어렵습니다.

 

따라서 단순히 L와 graph signal f를 곱하는 대신 f를 두 번 곱해 제곱 형태로 만들면, 그 값이 작을수록 neighbor node와 유사하다는 의미를 갖게 됩니다. 이 형태를 Laplacian Quadratic form이라고 합니다.

 

 

1) Graph Tasks

 

 

 

 

image 데이터에 관해서도 image classification, object detection 등 여러 가지 task가 존재하듯이, graph 데이터에 관련해서도 여러 가지 task가 존재합니다.

 

먼저 Graph Classification은 “그래프 자체”가 어느 속성에 속하는지 구분하는 것이고,

Edge Classification은 “주어진 edge”가 어느 속성에 속하는 것인지 구분하는 것입니다.

Link Prediction은 Edge Classification과 달리, node 간에 “edge 자체가 있을지 없을지”를 예측하는 task입니다.

마지막으로 Node Classification은 “주어진 node”가 어느 속성에 속할 것인지 구분하는 task로써 오늘 중점적으로 살펴볼 내용입니다.

 

2) Semi-supervised Learning

 

 

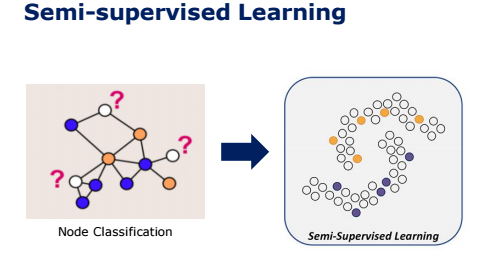
특히 Node Classification은 unlabeled 데이터에 대해서도 분류를 해야 하기 때문에 Semi supervised Learning이라 할 수 있습니다.

 

Semi Supervised Learning을 간단하게 설명하자면, label이 있는 데이터와 없는 데이터를 모두 사용하여 학습하는 것으로, 소규모의 labeled data를 통해 대량의 unlabeled data를 학습한다는 것이 특징입니다. Node Classification에서의 Semi supervised learning은 label이 붙어있는 않는 node에 대해서 labeled data를 이용해 분류하는 것입니다.

 

- Semi-supervised Learning의 방식 

 

그래프에서의 Semi-supervised learning은 그 방식에 따라 크게 두 가지로 나눌 수 있습니다.

 

먼저 Transductive learning은 그래프 상의 일부 node와 edge의 ground truth를 아는 상태에서 나머지 node와 edge의 값을 추정하는 것으로, 주어진 node들에 관해서만 예측 가능합니다. 저희가 오늘 살펴볼 GCN 또한 Transductive Learning을 사용합니다.

 

반면 Inductive Learning은 Ground Truth를 알고 있는 graph에 대해서 모델을 학습한 후, 새로운 graph에 대해 node와 edge의 값을 추정하는 것입니다. 다르게 말하자면 decision boundary를 학습하여 새로운 입력 값이 들어오더라도 예측 가능하도록 하는 방식입니다.

 

4) GNN 기본 원리 

 

 

GCN은 Graph network에 CNN에서의 Convolution 개념을 적용했습니다. 먼저 CNN에서의 특징 두 가지를 살펴보겠습니다.

 

(1) 먼저 CNN에서는 filter가 이동하면서 local feature들과 연산하고 activation map을 생성하므로 각 activation map의 pixel들은 global이 아닌 local feature들에 의해서만 학습된다고 볼 수 있습니다.

 

(2)두번째로, CNN에서는 image와 같은 input data에 동일한 weight를 갖는 동일 filter를 이동하면서 연산을 진행합니다.

 

 

GCN에서도 이런 두 성질이 그대로 반영됩니다.

 

만약 왼쪽과 같은 그래프가 있을 때 hidden state는 다음과 같이 update됩니다. GNN에서 Hidden state는 node feature matrix라고도 불리며, 행은 노드의 개수, 열은 특징의 개수를 가집니다.

 

이때 동일한 weight 벡터를 H1, h2, h3, h4가 공유하기 때문에 CNN의 weight sharing이라는 특징을 여기서도 볼 수 있습니다.

 

또한 인접행렬을 곱함으로써 각각의 H state는 자신과 연결된 state에 의해서만 영향을 받는다는 것을 보아, local feature들을 학습한다는 특징을 알 수 있습니다.

 

 

 

따라서 GNN에서의 Receptive Field는 graph에서 기준 노드로부터 몇 개 거리까지 떨어져 있는지를 의미합니다. 레이어를 한번 거치면 기준 노드로부터 거리가 1개 떨어진 이웃 노드까지, 또 한번 레이어를 거치면 기준 노드로부터 2개 떨어진 이웃 노드까지 보게 됩니다. 이렇게 레이어를 여러 번 거칠수록 더 넓은 범위의 노드를 참고할 수 있게 됩니다.

 

- Graph Convolution의 방식 두 가지 

 

 

 

Graph convolution은 크게 Spatial graph convolution과 Spectral graph convolution, 두 가지 방법이 있습니다.

 

Spatial graph convolution은 convolution 연산을 graph 위에서 직접 수행하는 방식으로, 각 노드와 가깝게 연결된 이웃 노드들에 한해서 convolution 연산을 수행합니다. 즉, 노드와 이웃 노드들을 특정 grid form으로 재배열하여 convolution 연산을 수행하는 것입니다.  Spatial graph convolution은 고정된 이웃 노드에서만 정보는 받아서 노드의 정보를 업데이트를 한다는 한계가 있습니다.

 

 그러나, 그래프에서의 한 노드의 정보는 고정된 이웃 노드 말고도 멀리 연결되어 있는 노드의 정보도 시간이 흐르면서 밀려 들어올 수 있는 것입니다. 이를 노드 간 message passing이라 합니다. 즉, 한 노드의 정보는 여러 노드의 signal이 혼재해 있는 것으로, 이를 time domain이 아닌 frequency 도메인으로 분석한다면, 한 노드 내에 혼재된 signal들을 여러 signal의 요소로 나눠서 node의 특징을 더 잘 추출할 수 있습니다. 이것에 관한 것이 바로 “Spectral Graph Convolution”입니다. 즉, signal을 노드의 feature라고 봤을 때, 한 노드 내에 혼재된 signal들을 여러 signal의 요소로 나눠서 node의 특징들을 더 잘 추출할 수 있습니다. 이를 수행할 수 있는 대표적인 방법이 푸리에 변환입니다. 또한 앞서서 살펴본 Laplacian Quadratic form은 이 분야에서 graph signal의 smoothness, 즉 frequency을 의미하며, quadratic form 값이 크면 graph signal 간의 difference가 큰 것이므로, high frequency를 가졌다고 볼 수 있습니다. 논문에서는 node간의 feature value 차이가 적은 관계를 원하기 때문에 Laplacian 값이 작은 것을 지향합니다.

오늘 볼 GCN 논문은 Spectral graph convolution에 속합니다.

 

 

Paper Reading 

 

1. Introduction 

 

 

Semi-supervised learning 중 하나인 Transductive Learning도 궁극적으로는 기존에 가지고 있던 Unlabeled Data에 대한 Label값을 찾는 것이 목표입니다.

 

이를 위해 기존에는 Graph based semi supervised learning 시에 과적합 되는 것을 막기 위해 Supervised Loss에 Graph Laplacian Regularization term은 더한 loss function을 사용했습니다. 이때 함수 f는 신경망과 같은 미분 가능한 함수, X는 노드 피쳐 벡터, A는 인접 행렬, D는 차수 행렬을 의미합니다. 여기서 델타는 차수 행렬 마이너스 인접 행렬로, 앞에서 말씀드렸던 라플라시안 행렬이 됩니다.

 

하지만 이 Loss function은 “만약 두 점이 가까이 위치한다면 비슷한 label값을 가져야 한다”는 가정 하에서 만들어졌기 때문에 Edge가 node Similarity 이외의 추가적인 정보를 담는 경우에는 제약이 있습니다.

 

 그렇기 때문에 본 논문에서는 그래프 구조에 직접적으로 이용할 수 있는 feed forward network model를 제안합니다. 또한 이 GNN을 어떻게 확장 가능한 semi-supervised  node classification으로 적용할지에 대해 다루게 됩니다.

 

 

2. Fast Approximation Convolutions on Graphs 

 

 

앞에서 오늘 소개드리는 GCN은 Graph convolution의 두 가지 방법 중에 Spectral 방식에 속한다고 말씀드렸습니다.

 

Spectral 방식은 그래프를 frequency domain으로 바꿔서 분석을 진행하는 것입니다. 즉, 한 노드 내에 혼재된 signal들을 여러 signal의 요소로 나눠서 node의 특징을 추출해내는 방법입니다. 그리고 그 분해하는 대표적인 방법이 푸리에 변환이라고도 말씀을 드렸습니다. 

 

먼저 signal x에 푸리에 변환을 적용해 signal, 여기서는 node의 특징들을 분리를 한 뒤, filter g_theta을 통해 원하는 정보만을 걸러낼 수 있습니다. Inverse를 통해 frequency domain으로 바꾼 그래프를 다시 원래의 domain으로 바꾸는 과정까지 거치면 Spectral convolution을 정의할 수 있게 됩니다.

 

 

또한 Chebyshev(체비쇼프) 다항식으로 필터 g_theta를 파란색 2번처럼 근사하여, 각 신호 x에 대한 필터 g_theta에 대한 곱, 즉 spectral convolution을 파란색 3번과 같이 근사할 수 있습니다.

 

 

 

2.2절에서는 2.1의 spectral graph convolution을 딥 러닝에 접목시키는 아이디어를 소개합니다. 딥 러닝의 뉴럴 네트워크 모델은 대부분 여러 개의 선형의 convolution 레이어를 쌓아서 만들지만 파란색 3번은 다항식이기 이러한 구조에 적합하지 않습니다. 따라서 이를 선형 모델로 만들기 위해서 논문에서는 위 식에서 K=1을 적용하여 선형 convolution 필터가 되고, 이 레이어를 여러 번 쌓는 구조를 생각했습니다.

 

파란색 4번의 두 파라미터 theta＇_0, theta＇_1​이 전체 그래프에 걸쳐서 공유하는 파라미터가 됩니다. 논문에서는 파라미터의 수를 줄이기 위해 빨간색 2번과 같이​ 하나로 통일하여 필터를 근사시켰습니다.

 

빨간색 3번의 값은 [0,2]의 범위를 갖게 되는데, 딥 뉴럴 네트워크에서 레이어를 반복해서 적용하면 exploding/vanishing gradient 문제가 발생했다고 합니다. 따라서 논문에서는 이 식에 대해서 다음과 같이 renormalization 트릭을 사용했습니다.

 

이 식을 통해서 최종적으로 파란색 6번과 같이 일반화하여 정의할 수 있습니다.

 

최종적으로 논문에서는 2-layer GCN Z을 사용했으며, 두번째 layer에서는 classification을 위해 softmax를 사용했습니다. 저자는 이 모델에서 data X가 가지고 있지 않은 정보를 인접행렬 A가 가지고 있을 때 더 강력할 것이라 기대한다고 말했습니다.

 

또한 semi supervised multi class classification에 대해서는 출력 Z에 대해 아래의 cross entropy를 통해 labeled data에 대해 evaluate했다고 합니다. 이때 Y는 label이 있는 노드의 인덱스들의 집합입니다.

 

( 이때 weight 두 개는 full batch로 gradient descent를 이용해서 학습했습니다 )

 

 

4. Related Works 

 

 

Related Works에서는 크게 Graph 기반의 Semi-supervised Learning과 그래프에 Neural Network를 적용한 연구들을 설명합니다.

먼저 Graph 기반의 Semi-supervised Learning로, Introduction에서 기존 연구로 함께 살펴 보았던 Graph Laplacian Regularization에 대한 연구들을 언급합니다. 또한 앞에서 말씀드렸던 것처럼 라플라시안 행렬과 같은 Matrix의 표현의 한계로 인해 Graph Embedding Model 등장했다는 흐름 또한 나옵니다.

 

 

다음으론, 그래프에 Neural Network를 적용한 연구들을 크게 세 분야로 나눠서 설명합니다. GNN과 GNN을 활용한 Node Classification, Spectral GNN에 대한 이전 연구들에 대해 언급합니다.

 

 

 

5. Experiments

 

 

 

 

실험은 이전의 SOTA 모델과 동일한 실험 세팅을 사용했으며 데이터 셋은 네 가지를 사용했습니다. 위 세개의 데이터는 Citation network 데이터 셋입니다. 여기서 NELL 데이터 셋은 entity 간의 관계를 나타낸 그래프로, directed graph이지만 GCN은 undirected graph만을 다룰 수 있기 때문에 undirected로 변형하여 사용하였다고 합니다.

구체적인 실험 세팅은 아래와 같습니다.

 

 

결과적으로 다른 node classification 모델들과의 성능 비교에서도 GCN이 모든 데이터셋에 대해서 가장 좋은 결과를 냈다고 합니다. 또한 모델 내에서도 중간 과정의 수식으로 학습을 진행했을 때의 결과보다 최종적으로 GCN에서 사용한 방법이 가장 좋은 성능을 냈습니다.

 

 

7. Future Works 

 

논문의 마지막에서는 향후 개선점에 대해서 3가지를 언급했습니다.

 

먼저 논문의 모델에서는 Full batch를 사용해서 큰 그래프에 대해선 GPU를 사용하지 못한다는 단점이 있었는데 이는 Mini batch로 나눈다면 해결할 수 있을 것이라고 제안합니다.

 

또한 이 모델은 현재 무방향 그래프만을 처리하기 때문에 이를 개선점으로 꼽았습니다.

 

마지막으로 현재는 Self connection과 이웃 노드와의 연결의 중요도를 같은 비율로 보았는데 이를 파라미터로 두어 학습 가능하도록 한다면 좋을 것이라고 제안했습니다.

 

 

 

 

Reference

 

https://paperswithcode.com/method/gcn

Papers with Code - GCN Explained

 

https://www.youtube.com/watch?v=YL1jGgcY78U