Graph Attention Network (GAT) 정리

Graph Attention Network (GAT) 정리

 

 

들어가기 전에....

 

Attention & Transformer 

 

https://asidefine.tistory.com/153

Seq2Seq & Attention & Transformer

 

GCN

 

https://asidefine.tistory.com/159

Semi-Supervised Classification with Graph Convolutional Networks (GCN) 정리 및 코드 분석

 

 

1. Introduction

 

 

 

굉장히 다양한 구조의 Graph를 다루기 위해 신경망을 확장하려는 시도는 지속되어 왔고, 초기 연구는 RNN으로 Graph 구조의 데이터를 다루고자 하였다. Graph Neural Network는 RNN의 일반화된 버전으로 소개되기 시작하였고 이후에 지속적으로 발전을 이어나갔다. 이후의 발전은 크게 2가지로 구분할 수 있을 것이다.

 

 

 

 

 

첫 번째는 Graph를 Spectral Representation으로 표현하는 것이다. Graph Laplacian의 eigen decomposition을 계산하는 Fourier domain으로 정의되는 합성곱 연산을 수행하는 것이 대표적인 방법이라고 할 수 있을 것인데, 이 연산을 통해 intense한 연산과 non-spatially localized한 filter를 만들어 낼 수 있다. 이러한 구조의 방법은 좀 더 세부적인 구조와 Feature의 특성을 반영하는데 특화되어 있지만 그 연산의 특성으로 인해, 새로운 구조의 Graph나 새로운 Node에 대해 대응하기 어려운 단점이 있다.

 

 그래프에서의 한 노드의 정보는 고정된 이웃 노드 말고도 멀리 연결되어 있는 노드의 정보도 시간이 흐르면서 밀려 들어올 수 있는 것입니다. 
이를 노드 간 message passing이라 합니다. 즉, 한 노드의 정보는 여러 노드의 signal이 혼재해 있는 것으로, 이를 time domain이 아닌 frequency 도메인으로 분석한다면, 한 노드 내에 혼재된 signal들을 여러 signal의 요소로 나눠서 node의 특징을 더 잘 추출할 수 있습니다. 이것에 관한 것이 바로 “Spectral Graph Convolution”입니다. 즉, signal을 노드의 feature라고 봤을 때, 한 노드 내에 혼재된 signal들을 여러 signal의 요소로 나눠서 node의 특징들을 더 잘 추출할 수 있습니다. 이를 수행할 수 있는 대표적인 방법이 푸리에 변환입니다. 

 

https://asidefine.tistory.com/159

Semi-Supervised Classification with Graph Convolutional Networks (GCN) 정리 및 코드 분석

 

 

 

두 번째는 Non-spectral 혹은 Spatial Representaion으로 정의할 수 있겠다. 이는 합성곱을 Graph에 직접적으로 적용하고, spatially close한 이웃 그룹에 대해 연산을 수행하는 방법을 의미한다. 이러한 방법의 대표적인 예시가 바로 GraphSAGE이다. 이러한 접근은 굉장히 scale이 큰 데이터에 대해 효과적인 접근으로 평가받고 있다. 

 

Spatial graph convolution은 convolution 연산을 graph 위에서 직접 수행하는 방식으로, 각 노드와 가깝게 연된 이웃 노드들에 한해서 convolution 연산을 수행합니다. 즉, 노드와 이웃 노드들을 특정 grid form으로 재배열하여 convolution 연산을 수행하는 것입니다.  Spatial graph convolution은 고정된 이웃 노드에서만 정보는 받아서 노드의 정보를 업데이트를 한다는 한계가 있습니다.

 

 

https://asidefine.tistory.com/169

Inductive Representation Learning on Large Graphs (GraphSAGE)

 

 

 

 

위와 같은 최근 연구의 연장선에서, 본 논문에서는 Graph 구조의 데이터에 대해 Node Classification을 수행하기 위해 Attention 기반의 구조를 소개할 것이다. (1) 연산은 효율적이며, (2) 이웃들에 대해 각기 다른 weight을 지정함으로써 다른 degree(Node가 갖는 이웃의 수)를 갖는 Graph Node에 적용될 수 있다는 장점을 지니고 있다. (3) 또한 이 모델은 Inductive Learning Problem에 직접적으로 적용될 수 있기 때문에 이전에 본 적이 없는 Graph에 대해서도 일반화할 수 있다는 큰 강점을 지닌다

 

 

 

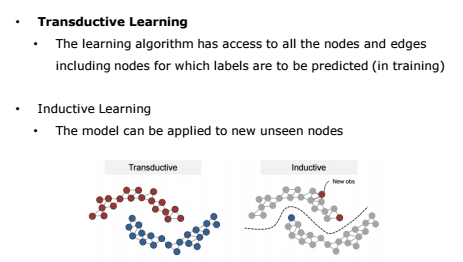
그래프에서의 Semi-supervised learning은 그 방식에 따라 크게 두 가지로 나눌 수 있습니다.
 
먼저 Transductive learning은 그래프 상의 일부 node와 edge의 ground truth를 아는 상태에서 나머지 node와 edge의 값을 추정하는 것으로, 주어진 node들에 관해서만 예측 가능합니다. 저희가 오늘 살펴볼 GCN 또한 Transductive Learning을 사용합니다.
 
반면 Inductive Learning은 Ground Truth를 알고 있는 graph에 대해서 모델을 학습한 후, 새로운 graph에 대해 node와 edge의 값을 추정하는 것입니다. 다르게 말하자면 decision boundary를 학습하여 새로운 입력 값이 들어오더라도 예측 가능하도록 하는 방식입니다.

 

 

 

 

2. GAT Architecture

 

2.1. Graph Attentional Layer

 

 

 

Expression 1.

e(ij) 는 i 노드와 j 노드의 Attention Coefficients

 

위 식은 Node i 에 대해 Node j 의 Feature가 갖는 중요도를 의미한다. 이 때 j 는 모든 Node를 의미하는 것은 아니고 Ni 즉, Node i 의 이웃에 대해서만 계산하게 된다. 이는 Masked Attention이라 할 수 있다. (Masked attention이란, e_{ij}를 계산할 때, j가 i의 이웃 노드일 경우(j∈Ni​)에 대해서만 계산을 수행하는 작업을 말한다. 위 식은 그래프의 구조에 대한 정보가 없기 때문에 모든 노드사이의 값이 계산되어버리게 된다. 그래서 여기서 그래프의 구조 정보를 주입하기 위해 masked attention을 수행한다. 이 논문에서 Ni​는 정확히 i의 1차 이웃(자기자신 포함), 즉 i와 직접 연결된 모든 이웃을 의미한다.)

각 h(i), h(j) 앞에 붙어 있는 W는 F x F’ 크기의 매트릭스로 각 노드를 임베딩하는 매트릭스
각 노드는 F개의 피쳐가 있는데 임베딩을 통해 F’ Dimension으로 바뀌게 된다.

 

 

Expression 2.

 

 

 서로다른 노드들의 attention coefficient 값들을 쉽게 비교하기 위해 다음과 같이 softmax를 통해서 normalize시킨다. 

최종적으로 softmax 함수를 통과하면 아래와 같은 Normalized Attention Score를 계산할 수 있다.

여기서 normalized attention coefficient \alpha_{ij}αij​가 바로 최종적으로 j의 각 feature가 i에게 영향을 주는 정도를 나타내는 값이 되는 것이다.
분모의 N(i)는 i 노드에 연결된 이웃 노드들의 집합 (i 도 포함된다)
알파가 의미하는 것은 이웃들의 전체 coefficient 합 중 e(ij)가 차지하는 비율(혹은 확률)

 

 

Expression 3.

 

이전 식에서 a 로 표기되었던 Attention Mechanism은 single-layer feedforward 신경망으로, 아래와 같이 학습 가능한 파라미터와 LeakyRELU activation 함수로 정의할 수 있다.

 

이 논문에서 사용한 self-attention 매커니즘 aa는 가중치를 벡터 \vec a\in \mathbb R^{2F'}a∈R2F′로 하고, activation function으로 LeakyReLU를 적용시킨 단일 feed-forward 뉴럴네트워크 레이어다. 위에서 언급했던 Bahdanau 어텐션과 흡사하게 concat을 사용해서 weight를 계산하였다.

 

여기서 \Vert∥는 concat을 나타내는데, 즉 두 W\vec h_i,W\vec h_jWhi​,Whj​벡터들을 \vec a^TaT로 한번에 선형변환시키고, LeakyReLULeakyReLU를 적용하여 e_{ij}eij​로 만들었다는 뜻이 된다.

 

조금 더 구체적으로 Attention Coefficient가 어떻게 나타나는지 표현되어 있다.
식의 안쪽에서부터 살펴보면 [Wh(i) // Wh(j)]가 의미하는 것은 두 임베딩 벡터의 Concat이다.
F’ + F’ 하여 2F’ 길이의 벡터를 single-layer로 forward 시킨다.
LeakyRelu는 음수에 대해서도 어느정도 값을 취하는 nonlinear activation function

 

Expression 4.

 

이렇게 계산된 각 노드들의 normalized attention coefficients 값을 이전레이어에서의 각 이웃들의 feature \vec h_jhj​를 선형변환시킨 값에 적용하여 모든 노드들의 최종 출력 feature \vec h'_ihi′​를 구하게 된다.

 

이렇게 계산된 Attention Score는 아래와 같이 Node i의 이웃의 중요도를 결정하여 Input 데이터를 재정의하게 된다.
F 개 피쳐의 h는 주변 노드들의 (attention * F’) 들의 합인 h’로 재정의 된다.

 

 

 

Expression 5.

 

여기서 self-attention 과정의 안정성을 위해서 transformer논문에서와 마찬가지로 multi-head attention을 적용한다. 결국 KK개의 각 헤드마다 위 식을 계산해서 따로 activation function을 적용시키고, 이를 모두 합치는 것이다. 
GAT 에서는 concat 한 임베딩 벡터를 feed forward 하는 어텐션 네트워크를 K개 가진다.
Attention Is All You Need (2017) 에서 제안된 multi-head attention mechanism
F’ 길이의 벡터를 K번 Concat 하여 K * F’ 길이의 벡터를 얻는다.

 

 

Expression 6.

마지막 multi-head attention 레이어는 concat이 필요없으므로, 다음과 같이 전체 head들의 attention에 대한 평균을 구하는 식으로 대체하고, 마무리 activation(classification의 경우에는 softmax 등)을 적용한다.

만약 h’ 뒤에 output을 위한 fc layer가 추가되는 것이 아닐 때 취하는 구조
Expression 5와 같이 concat 하는 것이 아니라 K개의 F’ 길이 벡터들을 합해준 뒤 평균

 

 

 

 

 

 

 

2.2. Comparisons to Related work 

 

 

 

GCN과 달리 GAT는 같은 이웃 집단의 Node에 대해 다른 중요도를 배정하기 때문에 Model Capacity를 개선할 수 있으며 해석에 있어서도 도움을 주게 된다.

 

Attention Mechanism은 Graph의 모든 Edge에 공유되어 적용되기 때문에 전체 Graph에 대한 접근 없이도 학습이 진행될 수 있으며 이에 따라 Inductive Learning을 가능하게 한다.

 

GraphSAGE는 각 Node에 대해 고정된 수의 이웃을 추출하기 때문에 계산량을 일정하게 유지하게 되는데, 이는 추론을 행할 때 전체 이웃집단에 대해 접근할 수 없게 만드는 현상을 초래한다. 사실 본 논문에서는 LSTM Aggregator의 성능이 가장 좋았다고 기술하고 있는데, 이는 이웃 집단 내에서 각 이웃사이의 순서가 중요하다는 것을 암시하는 것과 다름이 없다. 만약 다른 Max Pooling Aggregator나 Mean Pooling Aggregator를 사용하였는데, 각 이웃 Node 사이의 순서 혹은 다른 개별적인 특징이 중요하다면, GraphSAGE는 이러한 부분까지는 커버하지 못하는 단점을 지니게 된다. 본 논문에서 제시하는 GAT는 이러한 한계에서 자유로우며 이웃 전체에 대해 접근하면서도 효율적으로 학습을 진행할 수 있다는 장점을 지닌다.

 

 

 

 

 

3. Evaluation

 

 

평가에 대해서는 사용한 (3.1) Dataset들, (3.2) SOTA 방법들, (3.3) 실험 세팅들, (3.4)결과에 대해서 Transductive Learning과 Inductive Learning으로 나눠서 언급했다. 

 

 

 

3.1. Datasets

 

 

1) Transductive Learning 

 

3가지의 citation network dataset들을 사용했다 

 

(1) Cora

(2) Citeseer

(3) Pudmed

 

 

2) Inductive Learning 

 

(1) PPL (Protein-Protein Interaction)

 

 

=> 위 4가지 데이터셋의 특징은 Table 1에 잘 설명되어있음 

 

 

 

 

 

3.2. State-Of-The-Art Methods

 

1) Transductive Learning

 

비교 모델로 9가지 모델을 사용했다

 

 

먼저, GCN 등장 이전에 Graph 기반의 Semi-Supervised Learning 모델들 5가지가 있는데, 크게 (A) Explicit Graph Laplacian Regularization 방법을 사용한 모델과 (B) Graph Embedding-Based Model로 나눠진다. GCN 논문의 Related Works에서도 동일한 모델들이 언급된 바 있다.

 

( 라플라시안 행렬과 같은 Matrix의 표현의 한계로 인해 Graph Embedding Model 등장했다. )

 

 

A) Explicit Graph Laplacian Regularization 방법을 사용한 모델

 

   (1) LP (Label Propagation)

   (2) SemiEmb (Semi-supervised Embedding)

   (3) ManiReg (mainfold regularization)  

 

(B) Graph Embedding-Based Model

 

   (4) DeepWalk (Skip-gram based graph embeddings)

   (5) ICA (the Iterative classification algorithm)

   (6) Planetoid

 

 

 

 

다음으로, GCN 등장 이후 Graph Convolutional Network를 사용한 모델들 또한 비교 모델로 사용하였다. 

 

(7) GCN

(8) graph convolutional models utilising higher-order Chebyshev filters

(9) MoNet 

 

 

 

 

2) Inductive Learning 

 

비교 모델로 4가지의 supervised GraphSAGE inductive methods을 사용했다. 

 

(1) GraphSAGE-GCN : extending a graph convolution-style operation to the inductive setting

(2) GraphSAGE-mean : taking the elementwise mean value of feature vectors

(3) GraphSAGE-LSTM : aggregating by feeding theneighborhood features into an LSTM

(4) GraphSAGE-pool : taking the elementwise maximization operation of feature vectors transformed by a shared nonlinear multilayer perceptron

 

 

 

3.3. Experimental Setup

 

 

1) Transductive Learning

 

 

 

 

2) Inductive Learning 

 

 

 

 

 

 

 

3.4. Results

 

1) Transductive Learning

 

 

 

2) Inductive Learning 

 

 

 

 

 

4. Conclusions 

 

 

 

 

Summary 

 

 

1) We have presented graph attention networks (GATs), novel convolution-style neural networks that operate on graph-structured data, leveraging masked self-attentional layers

 

 

2) 행렬 연산을 하지 않고, 그래프에 있는 모든 노드들에 대해서 병렬화가 가능해서 계산이 효율적이다

[ The graph attentional layer utilized throughout these networks is computationally efficient (does not require costly matrix operations, and is parallelizable across all nodes in the graph) ]  

 

 

3) 각각 다른 이웃 노드에 다른 중요도를 할당할 수 있다 

[ allows for (implicitly) assigning different importances to different nodes within a neighborhood while dealing with different sized neighborhoods ] 

 

 

4) 그래프의 전체 구조에 의존하지 않는다 (inductive learning의 특징?)

[ does not depend on knowing the entire graph structure upfront—thus addressing many of the theoretical issues with previous spectral-based approaches ] 

 

 

5) Our models leveraging attention have successfully achieved or matched state-of-the-art performance across four
well-established node classification benchmarks, both transductive and inductive (especially, with completely unseen graphs used for testing)

 

 

 

 

 

Future Work

 

 

1) 큰 배치 사이즈에 대해서 다루는 것 

[overcoming the practical problems described in subsection 2.2 to be able to handle larger batch sizes]

 

2) attention mechanism과 관련하여 model interpretability에 대한 연구를 좀 더 진행하면 좋을 것 

[ A particularly interesting research direction would be taking advantage of the attention mechanism to perform a thorough analysis on the model interpretability ] 

 

3) node classification 분야 말고도 graph classification에 해당 방법 적용해봐도 좋을 것 같다 

[ Extending the method to perform graph classification instead of node classification would also be relevant from the application perspective ] 

 

4) edge의 feature들도 모델 구성에 포함한다면 더 많은 문제를 해결할 수 있을 것이다 

[ Extending the model to incorporate edge features (possibly indicating relationship among nodes) would allow us to tackle a larger variety of problems ] 

 

 

 

 

Reference

 

 

 

https://www.youtube.com/watch?v=NSjpECvEf0Y 

https://www.youtube.com/watch?v=shdNuppfClU 

https://docs.dgl.ai/en/0.6.x/tutorials/models/1_gnn/9_gat.html

Understand Graph Attention Network — DGL 0.6.1 documentation

https://www.dgl.ai/blog/2019/02/17/gat.html

Deep Graph Library

https://thejb.ai/gat/

Graph Attention Networks

https://chioni.github.io/posts/gat/

Graph Attention Networks (Pytorch)

https://greeksharifa.github.io/machine_learning/2021/05/29/GAT/

Python, Machine & Deep Learning

https://untitledtblog.tistory.com/174

[머신 러닝/딥 러닝] 그래프 어텐션 네트워크 (Graph Attention Network) 구조 및 설명

http://dmqa.korea.ac.kr/activity/seminar/296

고려대학교 DMQA 연구실