[GNN] 4-2. Convolutional Graph Neural Networks (ConvGNNs) 정리

 

 

[GNN] 4-2.  Convolutional Graph Neural Networks (ConvGNNs) 정리

 

 

 

1. Graph란?

- 왜 Graph?

- Graph의 종류

- Graph의 표현

- Graph Tasks

- Graph의 Motif 

 

 

2. GNN 이전의 Machine Learning을 활용한 Graph 학습 

- Node Feature

• Eigenvector centrality
• Betweenness centrality
• Closeness centrality
• .....

- Link Feature

• Distance-based feature
• Local neighborhood overlap
• Global neighborhood overlap

- Graph Feature

• Graphlet kernel
• Weisfeiler-Lehman Kernel 

 

3. Graph Representation Learning

- Node Embedding

- Graph Embedding 

 

 

4. GNN

- Recurrent Graph Neural Networks (RecGNNs)

- Convolutional Graph Neural Networks (ConvGNNs)

• Spectral Model
• Spatial Model 

- Graph AutoEncoders (GAEs) 

• Network Embedding
• Graph Generation

- Spatial-Temporal Graph Neural Networks (STGNNs)

• CNN Based 
• RNN Based
• CNN & RNN based Model 
• Attention based Model 

 

5. GNN의 Benchmark Datasets

- Citation Networks

- Biochemical Graphs

- Social Networks 

- Others

 

 

6. GNN Library

- Pytorch Geometric

- DGL 

 

 

 

 

---

 

 

들어가기 전에...

 

 

 Convolutional Graph Neural Networks (ConvGNNs) 

 

 

Convolutional Graph Neural Network는 이전의 Recurrent GNN 과 많이 연관되어있다. Recurrent GNN 에서는 같은 recurrent layer를 계속 반복하며 각 노드의 hidden state 를 일정 step 만큼 업데이트했었는데, Convolutional GNN 에서는 이 recurrent layer 대신에 각 convolutional layer 를 사용한다는 점이 다르다.

여기서 주목해야 할 부분은, Recurrent GNN 에서는 각 step 마다 동일한 레이어를 재귀적으로 사용하는 반면, Convolutional GNN 에서는 각 단계별 convolutional layer를 따로따로 적용한다는 점이다. 이로서 두 가지 다른 점을 생각할 수 있다.

 

1. Recurrent Layer 는 단계마다 동일한 가중치를 가진 레이어를 사용하는 반면, Convolutional Layer 는 각 단계별로 다른 가중치를 사용한다는 점이다.

이는 얼핏 보면 recurrent 방식이 개념적으로 더 맞지 않나? 생각이 들 수도 있다. Recurrent는 동일한 입장에서 hidden state 의 순환을 바라보는 느낌이 드는데, convolutional 방식은 여러 노드가 다 상황이 다른데, 각 단계별로 다른 가중치를 주는 것의 의미가 있나? 라는 느낌이 들기도 한다.
하지만 결국 convolutional 방식이 훨씬 더 결과가 좋았고, 이렇게 단계별 가중치가 유용하다는 것을 이해하는 관점에서 Convolutional GNN 을 살펴보면 좋을 것이다.

 

2. Recurrent GNN은 t번째 레이어를 구하기 위해서는 t번의 입력과 출력을 반복하면서 계산을 수행해야 하는 반면 반면, Convolutional GNN은 단순히 t개의 Convolutional Layer를 연결하여 한번에 output까지 구할 수 있다.

이는 Back propagation 을 할 때, 재귀적으로 가중치를 업데이트 할 필요 없이 한번에 업데이트가 가능하게 되어 연산이 훨씬 효율적으로 수행된다. 따라서 두 방식이 동일한 성능을 내더라도 Convolutional GNN이 훨씬 유용하게 사용될 수 있는 결정적인 이유가 된다.

 

 

 

 

Spectral Graph Convolution VS Spatial Graph Convolution 

 

 

 

일반적으로 Graph data에 Convolution을 적용하기 위해 크게 spectral과 spatial 두 가지 관점으로 접근한다. 

 

 

Spatial graph convolution은 convolution 연산을 graph 위에서 직접 수행하는 방식으로, 각 노드와 가깝게 연결된 이웃 노드들에 한해서 convolution 연산을 수행한다. 즉, 노드와 이웃 노드들을 특정 grid form으로 재배열하여 convolution 연산을 수행하는 것이다.  Spatial graph convolution은 고정된 이웃 노드에서만 정보는 받아서 노드의 정보를 업데이트를 한다는 한계가 있다.

 

 

 그러나, 그래프에서의 한 노드의 정보는 고정된 이웃 노드 말고도 멀리 연결되어 있는 노드의 정보도 시간이 흐르면서 밀려 들어올 수 있다. 이를 노드 간 message passing이라 한다. 즉, 한 노드의 정보는 여러 노드의 signal이 혼재해 있는 것으로, 이를 time domain이 아닌 frequency 도메인으로 분석한다면, 한 노드 내에 혼재된 signal들을 여러 signal의 요소로 나눠서 node의 특징을 더 잘 추출할 수 있다. 이것에 관한 것이 바로 “Spectral Graph Convolution”이다. 즉, signal을 노드의 feature라고 봤을 때, 한 노드 내에 혼재된 signal들을 여러 signal의 요소로 나눠서 node의 특징들을 더 잘 추출할 수 있다. 이를 수행할 수 있는 대표적인 방법이 푸리에 변환이다. 또한 Laplacian Quadratic form은 이 분야에서 graph signal의 smoothness, 즉 frequency을 의미하며, quadratic form 값이 크면 graph signal 간의 difference가 큰 것이므로, high frequency를 가졌다고 볼 수 있다. 따라서 node간의 feature value 차이가 적은 관계를 원하기 때문에 Laplacian 값이 작은 것을 지향한다.

 

Spectral 모델은 graph signal processing으로 접근하여 이론적인 기반이 튼튼하다는 장점이 있지만 spatial 모델들에 비해 효율성(efficiency), 일반화(generality), 그리고 유연성(flexibility)이 떨어진다는 단점이 있다. 이러한 이유로 보통은 spatial 모델을 더 선호한다고 한다.

 

첫 번째로 spectral 모델을 사용하기 위해서는 eigenvector를 사용하기 때문에 연산 시간이 많이 소비되고 배치 단위로 학습이 안되기 때문에 사이즈가 큰 데이터는 비효율적이라는 단점이 있다. 두 번째로 spectral 모델은 학습한 데이터의 Fourier basis를 기반으로 하기 때문에 새로운 데이터를 적용했을 때 기존에 가지고 있던 eigenbasis가 변해서 일반화가 떨어진다는 단점이 있다. 마지막으로 spectral 모델은 undirected graph에 제한되어 있기 때문에 다른 graph에는 사용할 수 없다는 단점이 있다.

 

종합해보면 결국 spectral은 이론적으로는 훌륭하나 써먹을 곳이 많지 않다는 말이다. 조금 더 다양한 graph에 적용할 수 있고 사이즈가 큰 데이터에도 학습할 수 있는 spatial 모델들이 더 유용한 것 같다.

 

Spectral 모델과 Spatial 모델 각각에 대해 아래에서 더 자세하게 설명하도록 한다. 

 

 

 

 

Spectral Models 

 

 

 

Spectral Graph Convolution 이해에 필요한 기본 개념들   

 

 

 

Spectral-based 방식은 그래프 신호 처리 이론을 기반으로 풀어낸 방식이다. Spectral-based 란 스펙트럼에 기반했다는 뜻인데, 여기서 스펙트럼이란 결국 여러가지 파동들의 집합이다. 왜 이러한 이름이 붙었는지 생각해보면, 이 spectral-based 방식에서는 결국 신호처리 이론의 푸리에 변환을 convolution으로 풀어내고 있다. 푸리에 변환이 결국 파동을 분해하는 변환이기 때문에, spectral이라는 이름을 갖게 된 것으로 보인다.

 

이 spectral-based 방식으로부터 GCN이 탄생하게 되었고, GCN이 좋은 결과를 내면서 이로부터 많은 연구들이 파생되고 있다. 따라서 spectral-based 방식은 GCN을 이해하기 위한 단계로서 접근하는 것이 좋다.

 

Spectral-based 방식은 기본적으로 무방향 그래프 전제로 하고, 그래프 정보를 normalized graph Laplacian matrix 로 표현하여 사용한다는 것이 특징이다.

 

 

이를 위해서 1) Normalized Graph Laplacian Matrix, 2) Graph Fourier Transform, 3) Graph Convolution, 4) Spectral Graph Convolution에 대해 먼저 개념을 짚고 넘어가도록 하겠다. 

 

 

 

 

1) Normalized Graph Laplacian Matrix 

 

(1) Laplacian Matrix

 

 

그래프는 일반적으로 행렬로 표현한다.

 

 첫번째로 인접 행렬은 노드 간의 연결 여부를 표현한다. 차수 행렬은 각 대각 행렬에 어떤 노드의 차수 정보, 즉 연결 edge의 개수만을 표현한다. 라플라시안 행렬은 차수 행렬에서 인접 행렬을 빼게 되면서 차수 행렬의 정보와 인접행렬의 정보를 모두 담게 된다. 식으로 나타내면 위와 같다.

 

하지만 이런 표현 방식은, 전체 노드의 개수가 많아질수록 행렬이 너무 커지기 때문에 이후에 그래프 임베딩이라는 개념을 통해 더 작은 차원으로 줄여서 사용한다.

 

 

 

(2) Normalized Graph Laplacian Matrix 

 

 

Normalized graph Laplacian matrix 는 라플라시안 행렬을 normalize 시켜준 행렬이다. 이는 다음과 같은 식으로 표현된다.

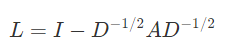
결국 기존 라플라시안 행렬에서 각 차수를 나타내던 (i,i)값이 1이 되고, 나머지 인접행렬 값이 차수에 대해서 normalize 시켜준 행렬이 된다. 실제 값은 다음과 같이 들어가게 된다.

 

이 normalize 된 라플라시안 행렬은 다음과 같이 분해될 수 있다.

 

여기서 UU는 각 고유벡터 u_iui​들을 고유값 크기순서로 정렬한 행렬 나타내고, Λ는 \Lambda_{ii}=\lambda_i, Λii​=λi​, Λij(i=j)​=0의 값을 갖는 행렬로, 결국 각 행을 λi​배 시켜주는 값이라고 생각하면 된다.

그런데, normalized graph Laplacian matrix 의 고유벡터는 서로 직교한다. 즉 다음과 같은 식이 성립하는 것이다.

 

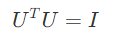
최종적으로 normalized graph Laplacian matrix인 L과, 여기에서 얻을 수 있는 U가 바로 spectral-based convolutional GNN 을 구하기 위해 사용된다.

 

 

 

laplacian quadratic form은 결과적으로 signal f의 "smoothness" 또는 "frequency"를 의미하며, signal f를 이러한 frequency의 집합으로 나타내어 연산하고자 하는 것이 spectral graph theory 이다. 그림의 오른쪽에서 볼 수 있듯이 quadratic form 값이 크면 graph signal 간의 difference가 큰 것이므로, high frequency를 가졌다고 볼 수 있다. 반대로 quadratic 값이 작으면 low frequency를 가졌다고 볼 수 있다. 그렇다면 Laplacian quadratic form의 solution은 무엇일까? 위 그림과 같이 form을 minimize하도록 하는 최적의 f를 구해 보면, f는 laplacian matrix L의 eigenspace에 속하는 벡터라고 한다. 즉 L의 eigenvector들이 해당 form을 최소화하는 것을 알 수 있다.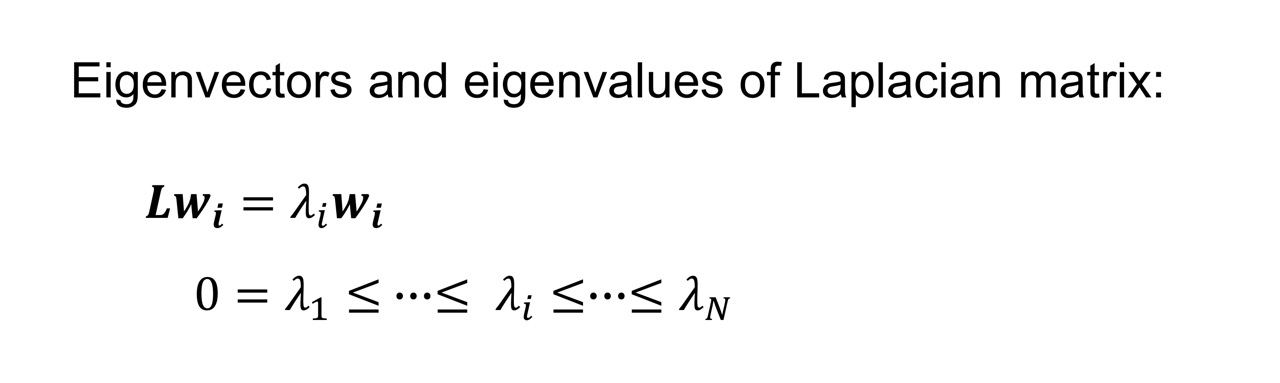  Laplacian matrix L의 eigenvector w와 eigenvalue λ는 위 그림과 같은 수식을 만족하게 되는데, 위 수식에서 w를 좌변으로 넘기면 위와 같은 수식이 된다! (u는 w와 같은 eigenvector) 즉 수식의 맨 왼쪽 항 u^T*L*u는 laplacian quadratic form과 같은 형태로 graph signal의 smoothness를 나타내고, 맨 오른쪽 항 λ는 L의 eigenvalue다. 즉 laplacian matrix L을 eigen decomposition하면, N개의 eigenvector와 eigenvalue를 얻을 수 있고, 각각의 eigenvalue는 각각 eigenvector signal u들의 smoothness를 의미하게 된다! 위 그림에서는 eigenvalue를 작은 것 부터 λ1, λ2, ...로 나열한 것이다.

 

 

 

2) Graph Fourier Transform

 

이제 graph signal의 smoothness를 의미하는 Normalized graph Laplacian Matrix 를 그래프 푸리에 변환에 사용한다. 여기서 푸리에 변환이 등장하는 이유는, 결국 convolution 연산을 푸리에 변환을 통해서 표현한다고 생각하면 된다. 그래프 신호 x∈Rn를 노드의 각 feature 벡터로 정의할 때, 각 원소 x_i는 i번째 노드의 값을 나타낸다. 이 경우에 그래프 푸리에 변환을 다음과 같이 정의할 수 있다.

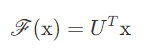
그래프 푸리에 변환은 입력 그래프 신호를 normalized graph Laplacian matrix를 통해 고유벡터들의 직교 공간으로 투사된다. 변환된 각 신호 }x^의 원소들은 변환된 공간에서의 위치를 나타낸다. 따라서 입력 신호 x는 다음과 같이 나타낼 수 있다.

 

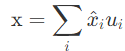
결론적으로, 위 그림과 같이 Graph Fourier Transform은 laplacian matrix L을 eigen decomposition하여 eigenvector들의 합으로 signal f를 표현하는 것이다. 즉 graph signal을 기존의 spatial공간에서 frequency를 나타내는 spectral공간으로 변환하는 것이다

이것의 의미는, 작은 eigenvalue를 갖는 eigenvector의 경우 graph를 더욱 smooth하게 나누는 기준이 되며, node간의 유사한 특징 정보를 담고 있다고 할 수 있다. 반대로 큰 eigenvalue를 갖는 eigenvector의 경우 node간 서로 다른 특징의 정보를 많이 담고 있다고 할 수 있다.

 

 

그렇다면 굳이 spatial domain에 있던 signal 정보를 왜 spectral domain으로 보내는 것일까? 그 이유는 graph signal을 frequency의 조합인 spectral domain에서 표현한 후, 다시 spatial domain으로 복원할 때 사용되는 filter를 학습함으로써 graph signal의 noise를 제거하고 필요한 성분만을 남겨 node를 embedding하기 위해서다.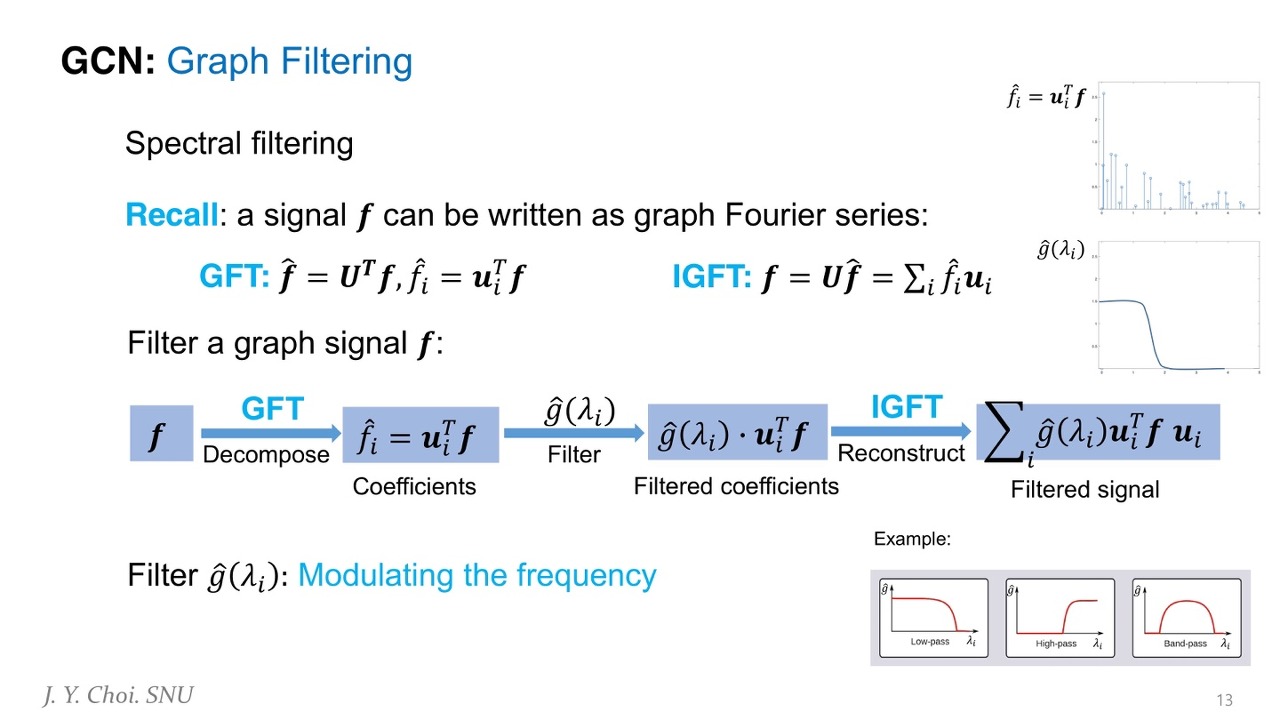 위 그림에서 볼 수 있듯이, GFT (Graph Fourier Transform)을 통해 signal f를 decompose한다. 이후 g(λi)를 곱하여 IGFT (Inverse Graph Fourier Transform)을 연산하고, 다시 spatial 공간으로 정보를 보내는데, 이 때 g(.)는 학습해야 할 filter 이다. filter g는 여러개의 frequency 신호 중 어떤 것을 사용해야 할 지 거르는 역할을 한다. 그림에서 오른쪽 위 두 그래프를 보시면, f^i는 fourier 계수(frequency)를, g^는 filter를 의미한다. 그림에서의 filter를 사용하면 앞 쪽에 있는 frequency들만 사용하고, 뒤 쪽에 있는 frequency들은 사용하지 않게 된다.

 

 

3) Graph Convolution

 

컨볼루션 필터를 g∈Rn라고 할 때, 그래프 컨볼루션 식은 다음과 같다.

 

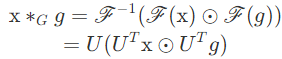
여기서 ⊙ 기호는 element-wise 곱셈, 즉 행렬에서 동일 위치에 있는 원소의 곱을 나타내고, ∗G​ 기호는 순환 합성곱인데, 그래프에서의 convolution 정도로 이해하면

 

4) Spectral Graph Convolution

 

여기서 각 convolution filter 를 gθ​=diag(UTg)라고 하면, spectral graph convolution 을 다음과 같이 정의할 수 있다.

 

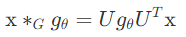
=> Spectral-based Convolutional GNN 은 위의 정의로부터 시작된다. 여기서 필터 gθ​를 어떻게 선택하냐가 중요하다.

 

 

 

 

Spectral Model들의 발전 과정 

 

 

Spectral Model들의 발전 과정은 아래와 같다. 

 

 

 

1. Spectral Convolutional Neural Network, Spectral CNN (2013)

2. Chebyshev Spectral CNN, ChebNet (2016)

3. Graph Convoluional Network, GCN (2017)

4. Adaptive Graph Convolutional Network, AGCN (2018)

5. Dual Graph Convolutional Network, DGCN (2018)

 

 

 

 

 

1. Spectral Convolutional Neural Network, Spectral CNN (2013)

 

Spectral CNN은 아래 식을 통해 convolution 연산을 한다. 이미지에서 사용되는 convolution과 마찬가지로 pooling을 통해 이웃들 간의 정보를 합하여 layer를 쌓아나간다.

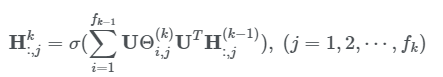
여기서 kk는 layer index이고 H(k−1)은 입력값인 graph signal을 말한다. 이때 초기 입력값은 H(0)=X이다. fk−1은 입력값의 채널 수이고 fk는 출력값의 채널 수 이다. Θ(k)i,j는 학습 파라미터로 단위 행렬이다.

Spectral CNN은 크게 세 가지 단점이 있다. 첫 번째로는 만약 학습된 모델에 기존 graph signal을 약간만 perturbation을 적용해도 eigenbasis가 바뀌어 버린다. 이는 spectral 모델의 큰 단점이기도 하다. 두 번째로는 학습한 filter를 다른 graph 구조를 가지고 있는 domain에 적용할 수 없다는 단점이 있다. 마지막으로 eigen-decomposition을 하기위한 연산 시간이 O(n3)으로 오래걸린다는 단점이 있다.

 

 

 

2. Chebyshev Spectral CNN, ChebNet (2016)

 

ChebNet은 이러한 Spectral CNN 연산시간을 Chebyshev polynomial of the first kind를 통해 filter를 근사하여 시간 복잡도를 O(m)으로 낮추었다. 또한 filter를 다항식으로 바꿔서 graph 사이즈와는 별개로 local feature를 추출할 수 있다는 장점이 있다. 

 

Chebyshev polynomial of the first kind는 convolution filter를 아래의 식과 같이 정의 할 수 있다

 

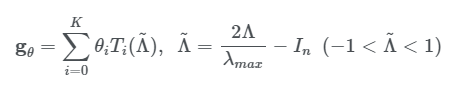
여기서 Λ~는 Λ를 [-1,1] 범위로 스케일링 한 값이다. T(⋅)은 Chebyshev polynomial function이다. Chebyshev polynomial of the first kind에서 다항식은 다음 식을 따른다.

 

 

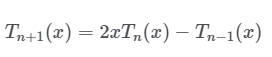
여기서 T0(x)=1 이고 T1(x)=x이다. 아래와 같이 정의할 수 있다.

 

 

 

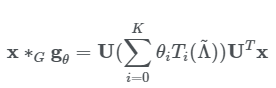
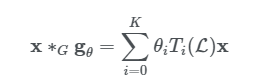
즉 Chebyshev(체비쇼프) 다항식으로 필터 g_theta를 파란색 2번처럼 근사하여, 각 신호 x에 대한 필터 g_theta에 대한 곱, 즉 spectral convolution을 파란색 3번과 같이 근사할 수 있다.

 

 

3. Graph Convoluional Network, GCN (2017)

 

 

GCN는 바로 위의 식에서  선형 필터를 적용하기 위해 위 ChebNet 을 1차 근사를 적용하고자 K=1로 λmax=2로 정의하였고 θ=θ0=−θ1로 parameter를 줄이면서 over-fitting을 방지하면서 식을 더 간단하게 정의할 수 있게 되었다. 마지막으로 renormalization trick을 적용하여 최종적으로 아래의 식과 같이 나타내었다. 

 

딥 러닝의 뉴럴 네트워크 모델은 대부분 여러 개의 선형의 convolution 레이어를 쌓아서 만들지만 파란색 3번은 다항식이기 이러한 구조에 적합하지 않다. 따라서 이를 선형 모델로 만들기 위해서 논문에서는 위 식에서 K=1을 적용하여 선형 convolution 필터가 되고, 이 레이어를 여러 번 쌓는 구조를 생각했다.

 

파란색 4번의 두 파라미터 theta＇_0, theta＇_1​이 전체 그래프에 걸쳐서 공유하는 파라미터가 된다. 논문에서는 파라미터의 수를 줄이기 위해 빨간색 2번과 같이​ 하나로 통일하여 필터를 근사시켰다.

 

빨간색 3번의 값은 [0,2]의 범위를 갖게 되는데, 딥 뉴럴 네트워크에서 레이어를 반복해서 적용하면 exploding/vanishing gradient 문제가 발생했다고 한다. 따라서 GCN 논문에서는 이 식에 대해서 다음과 같이 renormalization 트릭을 사용했다.

 

이 식을 통해서 최종적으로 파란색 6번과 같이 일반화하여 정의할 수 있다.

 

 

 

https://asidefine.tistory.com/159

Semi-Supervised Classification with Graph Convolutional Networks (GCN) 정리 및 코드 분석

 

 

 

 

4. Adaptive Graph Convolutional Network, AGCN (2018)

 

AGCN는 adjacency matrix로 표현되지 않은 노드 간의 관계를 학습하기 위해 “residual graph adjacency matrix”라는 것을 활용한다. 입력값으로 들어오는 두 노드의 거리를 학습 파라미터로 사용하여 학습한다.

 

 

 

5. Dual Graph Convolutional Network, DGCN (2018)

 

이름에서 알 수 있듯이 DGCN은 graph convolution 과정을 “parallel”하게 학습한다. 두 개의 layer는 서로 파라미터를 공유하고 ¯AA¯와 positive pointwise mutual information (PPMI)를 사용하여 graph에서 sampling을 통해 random walks를 적용한 후 노드들의 co-occurrence 정보를 계산한다. 

 

DGCN은 이러한 dual graph convolutional layers를 통해서 결과를 ensemble하여 layer를 깊게 쌓지 않아도 local 정보와 global 정보를 함께 encoding 할 수 있는 방법이다.

 

 

 

 

 

Spatial Models

 

 

이미지에서 사용하는 convolution과 유사하게 spatial 기반의 방법들은 노드들의 spatial 관계를 활용하여 학습하는 방법이다. Spatial 관계 라는건 중심 노드와 주변 노드의 관계를 말한다. Spatial 모델의 학습 과정은 convolution 과정을 통해서 중심 노드와 주변 노드의 representation을 학습하여 중심 노드의 representation을 업데이트 하는 방식을 말한다. 또다른 관점으로는 spatial 기반 GCN 모델은 앞서 설명한 RecGNNs의 information propagation 또는 message passing과 같은 개념으로 볼 수 있다. 즉, Spatial 모델 또한 edge를 통해 각 노드의 information을 전달하는 방식이다.

 

 

 

 

Spatial Model들

 

 

 

1. Neural Network for Graphs, NN4G (2009)

2. Contextual Graph Markov Model, CGMM (2018)

*

3. Diffusion Convolutional Neural Network, DCNN (2016)

4. Diffusion Graph Convolution, DGC (2018)

5. PGC-DGCNN (2018)

6. Partition Graph Convolution, PGC (2018)

*

7. Message Passing Neural Network, MPNN (2017)

8. Graph Isomorphism Network, GIN (2019)

* 

9. GraphSAGE (2017)

*

10. Graph Attention Network, GAT (2017)

11. Gated Attention Network, GaAN (2018)

*

12. GeniePath (2019)

*

13. Mixture Model Network, MoNet (2017)

*

14. PATCHY-SAN (2016)

*

15. Large-scale Graph Convolutional Network, LGCN (2018)

 

 

 

1. Neural Network for Graphs, NN4G (2009)

 

 

NN4G는 spatial 기반으로 GCN을 적용한 첫 논문이다. NN4G는 각 layer 마다 독립적인 parameter를 사용해서 ‘graph mutual dependency’를 학습하도록 하였다. (논문에서 언급된 ‘graph mutual dependency’가 정확히 어떤 의미인지는 명확하게 알 수 없었으나 layer 마다 서로 다른 parameter를 사용했기 때문에 layer 마다의 output이 서로 의존한다는 의미로 이해했다.) NN4G에서는 각 노드와 주변 노드 같의 합을 통해 aggregation 하였고 이전 layer의 output을 전달하기 위한 skip connection과 residual connection을 사용하였다. (논문에서 ‘and’ 로 작성되어 있어 두 connection이 서로 차이가 있는걸로 보는거 같지만 어떤 차이인지는 명확하지 않았다. 그냥 기존에 알고있는 skip connection을 적용했다 정도만 이해하고 넘어가도 좋다.) 아래의 식에서 f는 activation function을 의미한다. 

 

 

 

 

위 식을 보면 GCN과 유사한 것을 알 수 있다. 차이가 있다면 NN4G는 unnormalized adjacency matrix (A)를 사용한다는 것이다. 하지만 AA를 사용하게 되는 경우 hidden state node가 서로 다른 scale이 될 수 있는 단점이 있다.

 

 

 

2. Contextual Graph Markov Model, CGMM (2018)

 

CGMM은 NN4G의 아이디어를 기반으로 제안한 확률 모델이다. CGMM의 장점으로는 확률적인 해석이 가능하다는 장점이 있다. Survey 논문에서는 CGMM에 대해 크게 다루지 않았으므로 추가적으로 알고자 한다면 논문을 참고하는 것이 좋을 듯 하다.

 

 

****

 

 

3. Diffusion Convolutional Neural Network, DCNN (2016)

 

DCNN은 graph convolution 과정을 “diffusion process”로서 나타낸다. 여기서 diffusion process 란 하나의 노드에서 이웃 노드로 information을 전달할 때 특정 확률을 기반으로 전달하는 방법을 말한다. 이러한 과정을 여러 번 하다보면 특정 지점에서 수렴하게 되는 시점이 온다. DCNN은 아래 식과 같이 정의한다.

 

 

 

여기서 f(⋅)은 activation function이고 확률 matrix P∈Rn×n은 P=D^(−1)A로 계산된다. P에 대해 의미를 생각해보자면 각 노드의 연결된 이웃 노드에 대해 해당 노드의 degree로 나누어 1/degree(i)로 확률을 계산하였다고 생각할 수 있다.

 

여기서 알아야 할 점은 H(k)는 입력값 matrix인 X와 같은 차원의 matrix라는 점이고 H(k−1)로 부터 계산된 hidden representation이 아니라는 것이다. DCNN은 최종 output으로 H(1),H(2),⋯,H(K)를 모두 concatenate하여 사용한다.

 

 

 

 

4. Diffusion Graph Convolution, DGC (2018)

 

DGC는 아래 식과 같이 DCNN과 다르게 concatenate 대신 결과 값의 합을 사용하여 output을 나타낸다.

 

여기서 W(k)∈RD×F이고 f(⋅)은 activation function이다. 확률 matrix의 승을 사용한다는 의미는 멀리 있는 이웃 노드의 information이 중심 노드에 적게 영향을 주기 위함이라고 볼 수 있다.

 

 

 

5. PGC-DGCNN (2018)

 

PGC-DGCNN은 shortest path를 기반으로 먼 이웃의 기여도(contribution)을 키우는 방법이다. 여기서 사용되는 shortest path adjacency matrix는 S(j)로 정의하고 node v에서 node u까지의 shortest path가 j라면 S(j)v,u=1 아니면 0으로 한다. PGC-DGCNN에는 receptive field size를 조정하는 hyperparameter r이 있다. PGC-DGCNN은 아래의 식과 같이 나타낸다.

 

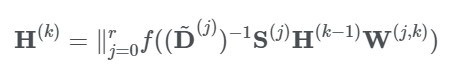
앞서 말한 ‘먼 이웃의 기여도를 키운다’는 위 식에서 볼 수 있듯이 receptive field의 크기에 따라 중심 노드로 부터 멀리 떨어진 노드도 함께 고려할 수 있다는 말이다. 하지만 PGC-DGCNN의 단점으로는 S(j)를 계산하는데 드는 시간 복잡도가 O(n3)이라는 점이다.

 

 

 

 

6. Partition Graph Convolution, PGC (2018)

 

PGC는 PGC-DGCNN과 다르게 단지 shortest path 만을 기준으로 하는 것이 아닌 특정한 기준(criterion)을 정해서 이웃 노드를 Q개의 그룹으로 나눠준다. 때문에 PGC에서는 Q adjacency matrix를 각각의 그룹별로 정의해서 사용한다. 그후 PGC의 연산과정을 앞서 소개한 GCN과 동일하다. Q 그룹 간의 결과값은 합으로 계산하여 산출한다. PGC는 아래 식과 같이 나타낼 수 있다.

 

 

****

 

7. Message Passing Neural Network, MPNN (2017)

 

MPNN은 spatial 기반의 ConvGNNs을 메인으로 하면서 graph convolution 과정을 노드에서 다른 노드로 information을 edge를 통해 바로 전달하게 하는 “message passing process”로써 나타낸 방법이다. MPNN은 K-step message passing을 반복한다. Message passing function는 아래의 식과 같이 정의할 수 있다.

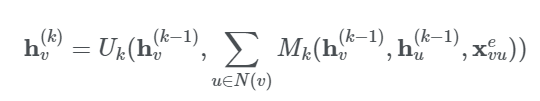
여기서 h(0)v=xv이고 Uk(⋅)와 Mk(⋅)은 학습 파라미터가 있는 function이다. 각 노드에 대해 hidden representation을 계산한 후에는 이 값에 output layer를 붙여서 node-level prediction 문제를 풀 수도 있고 readout function을 사용해서 전체 graph-level prediction 문제를 풀 수도 있다. 여기서 “readout function”이란 노드의 hidden representation을 통해 전체 graph의 representation을 뽑는 것을 말한다. readout function은 아래와  같이 정의할 수 있다.

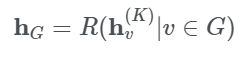
여기서 R(⋅)은 학습 파라미터가 있는 readout function을 말한다. MPNN은 Uk(⋅), Mk(⋅), 그리고 R(⋅)을 다른 형태로 나타내어 다른 GNNs에 적용할 수 있다. 하지만 미리 학습된 graph embedding 으로 다른 graph structure에 사용할 수 없다는 단점이 있다.

 

 

 

8. Graph Isomorphism Network, GIN (2019)

 

GIN은 중심 노드에 학습 parameter인 ϵ(k)를 더하여 이 값을 조정하며 MPNN의 단점을 보완하였다. GIN은 아래의 식과 같이 나타낼 수 있다.

 

 

논문에서는 GIN에 대한 내용은 이게 전부지만 ϵ(k)에 대하여 수식을 통해 이해한 바로는 주변 이웃의 수가 많아짐에 따라 중심 노드의 information이 사라질 수 있으니 ϵ(k)를 조정하여 중심 노드의 information 값을 키우는 것이 아닌가 싶다.

 

https://asidefine.tistory.com/186

How Powerful are Graph Neural Networks? (GIN) 정리

 

*****

 

9. GraphSAGE (2017)

 

GraphSAGE는 각 노드마다 이웃 노드의 수가 다양하게 존재하는데 모든 이웃 노드를 고려하는 것은 비효율적이기 때문에 일정한 이웃 노드 수를 고정하여 학습하는 방법이다. GraphSAGE의 graph convolution은 아래와 식을 통해 정의할 수 있다.

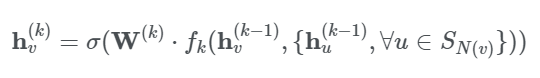
여기서 h(0)v=xv이고 fk(⋅)은 aggregation function, 그리고 SN(v)은 노드 v의 이웃 노드에 대한 샘플을 말한다. 이때 aggregation function은 mean, sum, 또는 max function과 같이 노드의 순서가 바뀌어도 같은 값이 나오도록 하는 invariant여야 한다.

 

 

https://asidefine.tistory.com/169

Inductive Representation Learning on Large Graphs (GraphSAGE) 정리

 

 

****

 

 

10. Graph Attention Network, GAT (2017)

 

 

GAT는 중심 노드에 대한 이웃 노드의 기여도를 계산하는 방법이 이웃 노드의 샘플을 정하는 GraphSAGE나 GCN과 같이 미리 고정된(pre-determined) 이웃 노드의 기여도와는 다르다. GAT는 일반적으로 사용되는 attention mechanisms을 사용한다. 단, graph에서는 연결된 두 노드의 상대적인 가중치를 학습하는 방식을 사용한다. GAT는 아래의 식과 같이 정의할 수 있다.

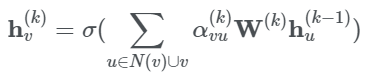
여기서 h(0)v=xv이다. Attention weight (α(k)vu)는 노드 v와 이웃 노드 u 와의 connective strength를 아래의 식과 같이 계산한다.

 

 

여기서 g(⋅)은 LeakyReLU activation function 이고 a는 학습 parameter이다. Softmax function은 노드 v의 모든 이웃의 attention weigth 합이 1이 되게하기 위해 사용하였다. GAT는 또한 multi-head attention을 사용하여 모델 성능을 더욱 향상 시킬 수 있고 실제로도 GraphSAGE 보다 node classification 문제에서 더 좋은 성능을 나타내었다.

 

 

https://asidefine.tistory.com/167

Graph Attention Network (GAT) 정리

 

 

11. Gated Attention Network, GaAN (2018)

GAT에서는 각각의 attention head의 기여도를 동일하게 적용하였지만 GaAN에서는 self-attention mechanism을 추가하여 각 attention head에 추가로 attention score를 계산하였다.

 

 

****

 

12. GeniePath (2019)

 

GeniePath는 LSTM 같은 gate mechanism을 통해 information을 조절하여 사용하는 방법이다. 별다른 소개가 더는 없어서 만약 내용이 궁금하다면 논문을 보는 것이 좋을 듯 하다.

 

 

****

 

13. Mixture Model Network, MoNet (2017)

 

MoNet은 노드의 이웃에 각각 다른 가중치를 주는 방법이다. 각 노드와 노드의 이웃들에 대한 상대적인 위치(relative position)를 나타낼 수 있는 ‘pseudo-coordinates’를 추가하여 위치에 따른 가중치를 부여할 수 있도록 학습하는 방법이다. 두 노드의 상대적인 위치가 주어지면 가중치 function은 각 위치에 맞는 가중치를 매핑하게 된다. 이러한 방식으로 graph filter의 가중치는 서로 다른 위치에 따른 가중치를 공유한다.

Pseudo-coordinates는 아마 transformer에서 사용되는 position-embedding 이나 CoordConv에서 사용되는 coordinate convolution과 같은 의미가 아닐까 싶다.

 

 

 

****

 

 

14. PATCHY-SAN (2016)

PATCHY-SAN은 서로 다른 위치에 따라 가중치를 주는 방법 중 하나이다. PATCHY-SAN은 특정한 기준과 학습 parameter에 순위를 매겨서 이웃 노드들의 순서를 정하여 서로 다른 가중치를 주는 방법이다. 노드의 순서는 “graph labeling”과 상위 q개의 이웃을 선정하여 결정한다. 여기서 graph labeling은 노드 degree, centrality, 그리고 Weisfeiler-Lehman color에 의해 정해진다. Weisfeiler-Lehman Algorithm은 두 그래프가 있을 때 isomorphic인지 아닌지 test하는 방법이기도 하고 또는 naive vertex classification에 사용 되기도 한다.

각 노드는 graph labeling 을 통해 q개의 정렬된 이웃 노드를 통해 graph-structure를 grid-structure로 변환할 수 있다. 이제 정렬된 이웃 노드의 순서에 맞게 1D convolutional filter를 사용하여 이웃 노드의 feature information을 aggregate 할 수 있다.

PATCHY-SAN의 단점으로는 ranking 기준이 graph structure에만 적용된다는 점이고 이는 연산량이 크다는 단점이 있다.

 

 

****

 

15. Large-scale Graph Convolutional Network, LGCN (2018)

LGCN은 노드의 feature information을 기준으로 이웃 노드의 순위를 정한다. LGCN의 feature matrix는 이웃 노드로 구성되어 있고 열을 기준으로 정렬하여 상위 q개를 중심 노드의 입력값으로 사용한다.

 

 

 

 

 

 

 

Spectral Model와 Spatial Model의 비교

 

 

 

Spectral-based는 기존의 그래프 신호처리 이론으로부터 발전하였고, 여기에서 GCN 또한 등장하였다는 점에서 의미를 갖는다. 하지만 결국 현재는 spatial-based 모델이 sepctral-based 보다 더 선호되는데, 그 이유는 다음과 같다

 

1. 계산의 효율성

Spectral-based 모델은 전체 그래프에 대해서 고유벡터를 계산하거나 다뤄야 한다. 하지만 spatial-based 모델은 이웃 노드들에 대해 직접 convolution 연산을 통해서 정보전달을 한다. 이는 그래프의 크기가 커질수록 전체 그래프를 다룰 필요가 없는 spatial-based 모델이 더 계산효율이 좋을 수밖에 없다.

 

 

2. 그래프의 변화에 대한 대응성

Spectral-based 모델은 푸리에 변환에 기반하여 그래프를 다룬다. 따라서 새로운 노드가 추가되는 등, 그래프가 바뀌는 경우는 아예 고유벡터부터 새로 계산해야 해서 모델을 다시 학습해야 한다. 즉 그래프가 고정되어있는 형태에 대해서만 다룰 수 있으며, 그래프의 관계가 변하는 경우를 다루기 어렵다. Spatial-based 모델은 해당하는 노드의 이웃들에 대해서만 새로운 계산을 해주면 된다.

 

3. 다룰 수 있는 그래프 종류

 

Spectral-based 모델은 전제부터 무방향 그래프로 제한되어있다. 하지만 Spatial-based 모델은 얼마든지 방향성 그래프를 다룰 수 있고, 여러 소스의 그래프 입력도 처리가 가능하다.

 

 

 

 

 

Reference

 

* 논문 설명

 

https://asidefine.tistory.com/159

Semi-Supervised Classification with Graph Convolutional Networks (GCN) 정리 및 코드 분석

https://asidefine.tistory.com/169

Inductive Representation Learning on Large Graphs (GraphSAGE) 정리

https://asidefine.tistory.com/167

Graph Attention Network (GAT) 정리

https://asidefine.tistory.com/186

How Powerful are Graph Neural Networks? (GIN) 정리

 

 

* Spectral Graph Convolution & Spatial Graph Convolution 

 

https://tootouch.github.io/research/gnn_summary/

Graph Neural Network 찍어먹기

 

https://ralasun.github.io/deep%20learning/2021/02/15/gcn/

Graph Convolutional Network에 대하여 - Spectral Graph Convolution · Ralasun Resarch Blog

https://ahjeong.tistory.com/14

GCN(Graph Convolutional Networks) 1편 : Graph Laplacian부터 Graph Fourier Transform까지 (Spectral Graph Theory)

https://ahjeong.tistory.com/15

GCN(Graph Convolutional Networks) 2편 : GNN model들의 발전 과정 - Spectral에서 Spatial Domain으로 (ChebNet, Spectral

https://thejb.ai/comprehensive-gnns-1/

Graph Neural Networks 개념정리 1 - 개요

https://thejb.ai/comprehensive-gnns-3/

Graph Neural Networks 개념정리 3 - Convolutional GNN (1) Spectral-based ConvGNN

https://thejb.ai/comprehensive-gnns-4/

Graph Neural Networks 개념정리 4 - Convolutional GNN (2) Spatial-based ConvGNN

https://velog.io/@thecho7/Graph-Neural-Network-3

Graph Neural Network - (3)

 

* Transductive Learning VS Inductive Learning 

 

https://towardsdatascience.com/inductive-vs-transductive-learning-e608e786f7d

Inductive vs. Transductive Learning

https://m.blog.naver.com/qbxlvnf11/221973639531

Transduction (Transductive Learning)과 Induction (Inductive Learning)

https://komputervision.wordpress.com/2020/03/24/inductive-learning-vs-transductive-learning/

inductive learning vs. transductive learning

https://junklee.tistory.com/127

Types of Learning in Machine Learning

https://thejb.ai/transduction/

Transduction